Question

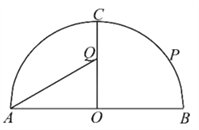
【题目】如图，某景区内有一半圆形花圃，其直径为，是圆心，且.在上有一座观赏亭，其中.计划在上再建一座观赏亭，记.

（1）当时，求的大小；

（2）当越大，游客在观赏亭处的观赏效果越佳，求游客在观赏亭处的观赏效果最佳时，角的正弦值.

Answer 1

【答案】（1）；（2）

【解析】

试题（1）先根据直角三角形解得，再根据正弦定理列关于三角方程，根据同角三角函数关系得，即得的大小；（2）根据正弦定理列关于的函数关系，利用导数求最值，即得结果.

试题解析：（1）设，由题，中，， ，

所以，在中，， ，

由正弦定理得，

即，所以 ，

则 ，所以，

因为为锐角，所以，所以，得；

（2）设，在中，， ，

由正弦定理得，即，

所以 ，

从而 ，其中，，

所以，

记，，；

令，，存在唯一使得，

当时，单调增，当时，单调减，

所以当时，最大，即最大，

又为锐角，从而最大，此时.

答：观赏效果达到最佳时，的正弦值为.