题目内容
在△ABC中,角A、B、C的对边分别为a、b、c,如果cos(2B+C)+2sinAsinB<0,那么三边长a、b、c之间满足的关系是( )
|
| A. | 2ab>c2 | B. | a2+b2<c2 | C. | 2bc>a2 | D. | b2+c2<a2 |
B.
【解析】在△ABC中,由cos(2B+C)+2sinAsinB<0可得,cos(B+B+C)+2sinAsinB<0.
∴cosBcos(B+C)﹣sinBsin(B+C)+2sinAsinB<0,即 cosBcos(π﹣A)﹣sinBsin(π﹣A)+2sinAsinB<0.
∴﹣cosBcosA﹣sinBsinA+2sinAsinB<0,﹣cosBcosA+sinBsinA<0.
即﹣cos(A+B)<0,cos(A+B)>0.
∴A+B< ,∴C>
,∴C> ,故△ABC形状一定是钝角三角形,故有 a2+b2<c2 .
,故△ABC形状一定是钝角三角形,故有 a2+b2<c2 .
故选 B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 ,则
,则 的值是( )
的值是( )
|
| A. | 9 | B. | ﹣9 | C. |
| D. |
|
函数f(x)=log2(1+x),g(x)=log2(1﹣x),则f(x)﹣g(x)是( )
|
| A. | 奇函数 | B. | 偶函数 |
|
| C. | 既不是奇函数又不是偶函数 | D. | 既是奇函数又是偶函数 |
 -
- )·(
)·( )=0,则DABC的形状一定为___________.
)=0,则DABC的形状一定为___________.

 ,函数
,函数 .
. 时,写出
时,写出 的增区间;
的增区间; ,求
,求 ,使函数
,使函数 在区间(0,6)内的图象上存在两点,在该两点处的切线互相垂直?若存在,求
在区间(0,6)内的图象上存在两点,在该两点处的切线互相垂直?若存在,求
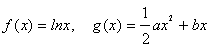
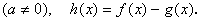
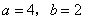 时,求
时,求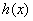 的极大值点;
的极大值点;  的图象
的图象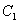 与函数
与函数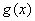 的图象
的图象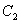 交于
交于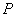 、
、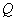 两点,过线段
两点,过线段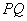 的中点做
的中点做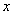 轴的垂线分别交
轴的垂线分别交 、
、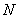 ,证明:
,证明: ,则
,则 .
. B.
B. C.
C. D.
D.
