题目内容
求下列函数的单调区间:(1)y=
解析:将原函数“拆”成两个简单的函数,再依据复合函数的单调性求解.
解:(1)令u=x2-4x-2,则y=0.5u.因为y=0.5u为减函数,所以y=![]() 与u=x2-4x-2的单调性相反.又由u=x2-4x-2=(x-2)2-6得u=x2-4x-2在(-∞,2]为减函数,在[2,+∞)为增函数.所以y=
与u=x2-4x-2的单调性相反.又由u=x2-4x-2=(x-2)2-6得u=x2-4x-2在(-∞,2]为减函数,在[2,+∞)为增函数.所以y=![]() 在(-∞,2)为增函数,在[2,+∞)为减函数;
在(-∞,2)为增函数,在[2,+∞)为减函数;
(2)令u=1+![]() ,则y=2u,因为y=2u为增函数,所以y=
,则y=2u,因为y=2u为增函数,所以y=![]() 的单调性与u=1+
的单调性与u=1+![]() 的单调性相同.因为u=1+
的单调性相同.因为u=1+![]() (x≠0)所以在(-∞,0)及(0,+∞)上均为减函数,所以y=
(x≠0)所以在(-∞,0)及(0,+∞)上均为减函数,所以y=![]() 的单调递减区间为(-∞,0)和(0,+∞).
的单调递减区间为(-∞,0)和(0,+∞).

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 ; (2)y=
; (2)y= tan2x+1;
tan2x+1;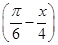 .
.