题目内容
已知函数f（x）=2cos2x+2
sinxcosx（x∈R）．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）设△ABC的内角A，B，C的对应边分别为a，b，c，且f（A）=2，b=1，且△ABC的面积为
，求边a的值．
| 3 |
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）设△ABC的内角A，B，C的对应边分别为a，b，c，且f（A）=2，b=1，且△ABC的面积为
| 3 |
考点：三角函数中的恒等变换应用,正弦函数的图象,正弦定理
专题：常规题型,三角函数的图像与性质,解三角形
分析：第（Ⅰ）问求函数的单调区间，要先把函数化成标准形式，即化成y=Asin（ωx+φ）+B的形式；第（Ⅱ）问根据f（A）=2求出角A，然后根据△ABC的面积为
，结合余弦定理求出a的值．
| 3 |
解答：
解：（Ⅰ）f（x）=2cos2x+
sin2x=cos2x+
sin2x+1=2sin（2x+
）+1
令-
+2kπ≤2x+
≤
+2kπ，k∈Z
解得，kπ-
≤x≤kπ+
，k∈Z
∴f（x）的递增区间为[kπ-
，kπ+
]（k∈Z）
（Ⅱ）由f（A）=2sin（2A+
）+1=2，得A=
S△ABC=
bcsinA=
∴c=4，
由余弦定理得a2=1+42-2×1×4×cos
∴a=
．
| 3 |
| 3 |
| π |
| 6 |
令-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得，kπ-
| π |
| 3 |
| π |
| 6 |
∴f（x）的递增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
（Ⅱ）由f（A）=2sin（2A+
| π |
| 6 |
| π |
| 3 |
S△ABC=
| 1 |
| 2 |
| 3 |
∴c=4，
由余弦定理得a2=1+42-2×1×4×cos
| π |
| 3 |
∴a=
| 13 |
点评：本题考查了求函数的单调区间，关键是化成标准形式；还考查了解三角形，注意根据条件选择适当的面积公式及正余弦定理．
练习册系列答案
相关题目
若定义在[-a，a]上的奇函数f（x）同时也是减函数，则函数y=f（-x）在[-a，a]上（ ）
| A、既是奇函数又是增函数 |
| B、既是奇函数又是减函数 |
| C、是偶函数且先增后减 |
| D、是偶函数且先减后增 |
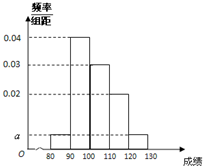为了分析我校市二模文科数学的成绩，现抽样统计了20位同学的数学成绩，形成了如图所示的频率分布直方图，其中成绩的分组区间是：[80，90），[90，100），[100，110），[110，120），[120，130]