题目内容
椭圆C的两个焦点分别为F1(-1,0)和F2(1,0),若该椭圆C与直线x+y-3=0有公共点,则其离心率的最大值为
- A.
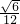
- B.

- C.

- D.
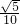
C
分析:根据 ,可得a越小e越大而椭圆与直线相切时a最小,将直线方程与椭圆方程联立,即可求得结论.
,可得a越小e越大而椭圆与直线相切时a最小,将直线方程与椭圆方程联立,即可求得结论.
解答:由题意,c=1,
∴ ,
,
∴a越小e越大,而椭圆与直线相切时,a最小
设椭圆为 ,把直线x+y-3=0代入,化简整理可得(2m-1)x2+6mx+10m-m2=0
,把直线x+y-3=0代入,化简整理可得(2m-1)x2+6mx+10m-m2=0
由△=0,解得:m=5,
于是a= ,
,
故选C.
点评:本题考查直线与椭圆的位置关系,考查椭圆的几何性质,解题的关键是确定椭圆与直线相切时a最小.
分析:根据
 ,可得a越小e越大而椭圆与直线相切时a最小,将直线方程与椭圆方程联立,即可求得结论.
,可得a越小e越大而椭圆与直线相切时a最小,将直线方程与椭圆方程联立,即可求得结论.解答:由题意,c=1,
∴
 ,
,∴a越小e越大,而椭圆与直线相切时,a最小
设椭圆为
 ,把直线x+y-3=0代入,化简整理可得(2m-1)x2+6mx+10m-m2=0
,把直线x+y-3=0代入,化简整理可得(2m-1)x2+6mx+10m-m2=0由△=0,解得:m=5,
于是a=
 ,
,
故选C.
点评:本题考查直线与椭圆的位置关系,考查椭圆的几何性质,解题的关键是确定椭圆与直线相切时a最小.

练习册系列答案
相关题目