题目内容
已知函数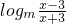 ,x∈[α,β],(其中a>0).
,x∈[α,β],(其中a>0).
(1)证明:a>3;
(2)问是否存在实数m,使得自变量x在定义域[α,β]上取值时,该函数的值域恰好为[logm(mβ-m),logm(mα-m)],若存在,求出实数m的取值范围,若不存在,请说明理由.
解:(1)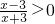 ?x<-3,或x>3,
?x<-3,或x>3,
∵f(x)定义域为[α,β]且α>0,
∴α>3. …(2分)
(2)∵3<α<β,m>0,
∴m(α-1)<m(β-1),而loga m(α-1)<logam(β-1),
∴0<m<1,…(4分)
设β≥x1>x2≥α,有 =
= >0,
>0,
∴当0<m<1时,f(x)在[α,β]上单调递减. …(7分)
又f(x)在[α,β]上的值域为[logm(mβ-m),logm(mα-m)],
∴
即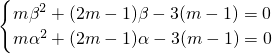 又β>α>3,…(10分)
又β>α>3,…(10分)
即α,β是方程mx2+(2m-1)x-3(m-1)=0大于3的两个不相等的实数根,…(11分)
∴ 解之得0<m<
解之得0<m<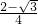 ,…(15分)
,…(15分)
因此,当0<m<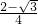 时,满足题意条件的m存在. …(16分)
时,满足题意条件的m存在. …(16分)
分析:(1)由题设条件,求出函数的定义域,再由题设条件x∈[α,β],(其中α>0)即可得出α>3.
(2)由题意,若存在这样的m,使得自变量x在定义域[α,β]上取值时,该函数的值域恰好为[logm(mβ-m),logm(mα-m)],可先确定函数的单调性,确定出函数的最值,由最值建立起方程求参数m的取值范围即可.
点评:本题的考点是对数函数图象与性质的综合运用,考察了对数型函数的单调性的判断,对数定义域的求法,解题的关键理解题意,判断出函数的单调性是本题的重点,本题考查了转化的思想,由题意,将题设条件正确转化对顺利解题很重要.
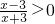 ?x<-3,或x>3,
?x<-3,或x>3,∵f(x)定义域为[α,β]且α>0,
∴α>3. …(2分)
(2)∵3<α<β,m>0,
∴m(α-1)<m(β-1),而loga m(α-1)<logam(β-1),
∴0<m<1,…(4分)
设β≥x1>x2≥α,有
 =
= >0,
>0,∴当0<m<1时,f(x)在[α,β]上单调递减. …(7分)
又f(x)在[α,β]上的值域为[logm(mβ-m),logm(mα-m)],
∴

即
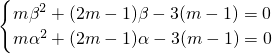 又β>α>3,…(10分)
又β>α>3,…(10分)即α,β是方程mx2+(2m-1)x-3(m-1)=0大于3的两个不相等的实数根,…(11分)
∴
 解之得0<m<
解之得0<m<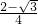 ,…(15分)
,…(15分)因此,当0<m<
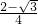 时,满足题意条件的m存在. …(16分)
时,满足题意条件的m存在. …(16分)分析:(1)由题设条件,求出函数的定义域,再由题设条件x∈[α,β],(其中α>0)即可得出α>3.
(2)由题意,若存在这样的m,使得自变量x在定义域[α,β]上取值时,该函数的值域恰好为[logm(mβ-m),logm(mα-m)],可先确定函数的单调性,确定出函数的最值,由最值建立起方程求参数m的取值范围即可.
点评:本题的考点是对数函数图象与性质的综合运用,考察了对数型函数的单调性的判断,对数定义域的求法,解题的关键理解题意,判断出函数的单调性是本题的重点,本题考查了转化的思想,由题意,将题设条件正确转化对顺利解题很重要.

练习册系列答案
相关题目
已知函数f(x)=
,则它是( )
| ||
| |x-3|-3 |
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |
已知函数f(x)=
则“-2≤a≤0”是“f(x)在R上单调递增”的( )
|
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |