题目内容
设函数 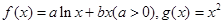
(Ⅰ)若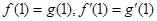 ,是否存在k和m,使得
,是否存在k和m,使得 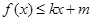 ,
,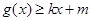 ,若存在,求出k和m的值,若不存在,说明理由
,若存在,求出k和m的值,若不存在,说明理由
(Ⅱ)设 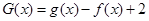 有两个零点
有两个零点  ,且
,且 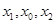 成等差数列,
成等差数列, 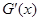 是 G (x)的导函数,求证:
是 G (x)的导函数,求证: 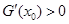
(Ⅰ) 存在k=2,m=-1;(Ⅱ)见解析
解析试题分析:(Ⅰ)先求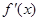 ,然后根据条件很容易求出a,b,此时会发现
,然后根据条件很容易求出a,b,此时会发现 和
和 图象有一个公共点(1,1),根据问题:是否存在k和m,使得
图象有一个公共点(1,1),根据问题:是否存在k和m,使得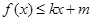 ,
,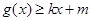 ,也就是找到一条直线要同时满足这两个不等式.根据存在的公共点可以想到是否是过这一点的直线,故先求出还
,也就是找到一条直线要同时满足这两个不等式.根据存在的公共点可以想到是否是过这一点的直线,故先求出还 在(1,1)的切线,然后去验证它是否同时满足
在(1,1)的切线,然后去验证它是否同时满足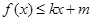 ,
,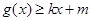 即可.(Ⅱ)先求出
即可.(Ⅱ)先求出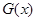 ,根据条件x1,x2是它的两个零点,所以x12?alnx1?bx1+2=0且x22?alnx2?bx2+2=0.根据所要证的结论:
,根据条件x1,x2是它的两个零点,所以x12?alnx1?bx1+2=0且x22?alnx2?bx2+2=0.根据所要证的结论: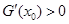 ,所以需要求
,所以需要求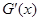 ,利用x1+x2=2x0,将
,利用x1+x2=2x0,将 用x1,x2表示出来,然后判断它是否大于0即可.
用x1,x2表示出来,然后判断它是否大于0即可.
试题解析:(Ⅰ)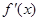 =
=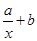 ,
,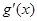 =
= ,由
,由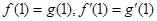 得:a+b=2, b=1,解得,解得a=b=1.∴
得:a+b=2, b=1,解得,解得a=b=1.∴ =
= .
.
因 与
与 有一个公共点(1,1),易求得函数
有一个公共点(1,1),易求得函数 =
= 在点(1,1)的切线方程为
在点(1,1)的切线方程为 .
.
下面验证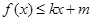 ,
,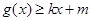 都成立即可.
都成立即可.
设h(x)=lnx+x-(2x-1)=lnx-x+1,所以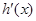 =
=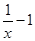 =
=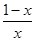 .
.
x∈(0,1)时,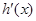 >0;x∈(1,+∞)时,
>0;x∈(1,+∞)时,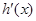 <0,∴x=1时,
<0,∴x=1时,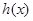 取最大值
取最大值 =0;
=0;
∴lnx+x≤2x-1恒成立,即 ≤
≤ 2.
2.
由于 ,得
,得 ,∴
,∴ ≥
≥ 恒成立.
恒成立.
故存在这样的k,m,且k=2,m=-1. 6分
(Ⅱ)因为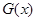 =
= =
= ,有两个零点x1,x2,
,有两个零点x1,x2,
则x12?alnx1?bx1+2=0且x22?alnx2?bx2+2=0,
两式相减得,x12? x22-a(lnx1? lnx2)-b(x1?x2)=0,
所以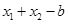 =
= ,又因为x1+x2=2x0,
,又因为x1+x2=2x0,
因为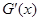 =
=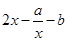 ,所以
,所以 =
=
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
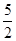 x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+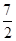 x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数). ,函数
,函数 (
( 为自然对数的底数).
为自然对数的底数). ,求函数
,求函数 的单调区间;
的单调区间; ,求
,求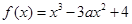 ,其中
,其中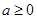 。
。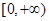 上的最小值。
上的最小值。 ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数. 是函数
是函数 的导函数,求函数
的导函数,求函数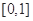 上的最小值;
上的最小值; ,函数
,函数 内有零点,求
内有零点,求 的取值范围。
的取值范围。 满足:①在
满足:①在 时有极值;②图像过点
时有极值;②图像过点 ,且在该点处的切线与直线
,且在该点处的切线与直线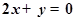 平行.
平行.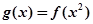 的单调递增区间.
的单调递增区间. 的图象如图所示,则
的图象如图所示,则 .
. 
 在点
在点 处的切线方程是
处的切线方程是  的导数为
的导数为 ,则
,则 = 。
= 。