题目内容
已知函数f(x)=x3+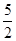 x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+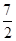 x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数).
(1)若g(x)在x=l处的切线方程为y=kx-5(k为常数),求b的值;
(2)设函数f(x)的导函数为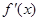 ,若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
,若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
(3)令F(x)=f(x)-g(x),若函数F(x)存在极值,且所有极值之和大于5+1n2,求a的取值范围.
(1) ;(2)
;(2) ;(3)
;(3)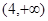 .
.
解析试题分析:
解题思路:(1)求导,利用导数的几何意义得到 解
解 即可;(2)求导,根据条件列出关于
即可;(2)求导,根据条件列出关于 的方程组,消去
的方程组,消去 ,化成关于
,化成关于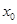 的一元三次方程,构造函数,进行求导,利用三次方程有唯一解进行求
的一元三次方程,构造函数,进行求导,利用三次方程有唯一解进行求 的范围;(3)构造函数,进行求导,将函数有极值转化为导函数为0有两个不相等的实根进行求解.
的范围;(3)构造函数,进行求导,将函数有极值转化为导函数为0有两个不相等的实根进行求解.
规律总结:三次函数零点的个数的判定:首先利用导数求出三次函数的极值,设极小值为 ,极大值为
,极大值为 ;①若
;①若 ,则有三个不等的零点;②若
,则有三个不等的零点;②若 或
或 ,则有两个不等的零点;③若
,则有两个不等的零点;③若 或
或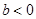 ,则有一个零点.
,则有一个零点.
试题解析:(1)∵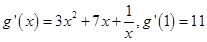 所以直线
所以直线 的
的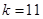 ,当
,当 时,
时, ,将(1,6)代入
,将(1,6)代入 ,得
,得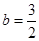 .
.
(2) ,由题意知
,由题意知 消去
消去 ,
,
得 有唯一解.
有唯一解.
令 ,则
,则 ,
,
所以 在区间(-∞,-
在区间(-∞,- ),区间(-
),区间(- ,+∞)上是增函数,在
,+∞)上是增函数,在 上是减函数,
上是减函数,
又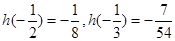 ,故实数
,故实数 的取值范围是
的取值范围是 .
.
(3)
因为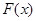 存在极值,所以
存在极值,所以 在
在 上有根即方程
上有根即方程 在
在 上有根.
上有根.
记方程 的两根为
的两根为 由韦达定理
由韦达定理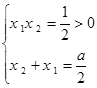 ,所以方程的根必为两不等正根.
,所以方程的根必为两不等正根. 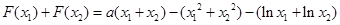


 所以
所以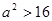 满足方程
满足方程 判别式大于零
判别式大于零
故所求取值范围为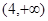 .
.
考点:1.导数的几何意义;2.利用导数研究函数的零点个数;3.利用导数研究函数的极值.

练习册系列答案
相关题目
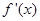 存在,且导函数
存在,且导函数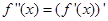 ,若
,若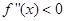 在D上恒成立,则称f(x)在D上为凸函数.以下四个函数在(0,
在D上恒成立,则称f(x)在D上为凸函数.以下四个函数在(0,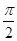 )上是凸函数的是_____ ___.(把你认为正确的序号都填上)
)上是凸函数的是_____ ___.(把你认为正确的序号都填上) 题满分12分)
题满分12分)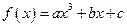
 为奇函数,其图象在点
为奇函数,其图象在点
 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数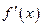 的最小值为
的最小值为
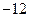 .
. 求
求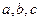 的值
的值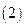 .求函数
.求函数 的单调递增
的单调递增 区间,极大值和极小值,并求函数
区间,极大值和极小值,并求函数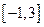 上的最大值与最小值.
上的最大值与最小值.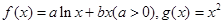
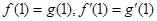 ,是否存在k和m,使得
,是否存在k和m,使得 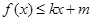 ,
,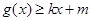 ,若存在,求出k和m的值,若不存在,说明理由
,若存在,求出k和m的值,若不存在,说明理由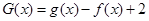 有两个零点
有两个零点  ,且
,且 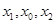 成等差数列,
成等差数列, 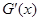 是 G (x)的导函数,求证:
是 G (x)的导函数,求证: 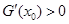
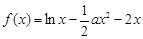 (
( ).
).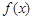 在定义域内单调递增,求实数
在定义域内单调递增,求实数 ,且关于
,且关于 的方程
的方程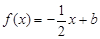 在
在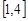 上恰有两个不等的实根,求实数
上恰有两个不等的实根,求实数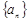 满足
满足 ,
,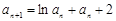 (
(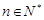 ),求证:
),求证: .
.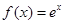 ,
,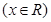 .
. 在点
在点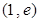 处的切线方程;
处的切线方程;  与曲线
与曲线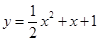 有唯一公共点;
有唯一公共点;  ,比较
,比较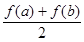 与
与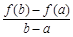 的大小, 并说明理由.
的大小, 并说明理由.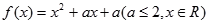 ,
, ,
,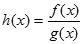
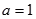 时,求
时,求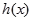 的单调区间
的单调区间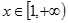 上是递减的,求实数
上是递减的,求实数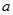 的取值范围;
的取值范围; 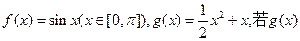 图像在点
图像在点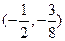 的
的 图像在点M处的切线平行,则点M的坐标为 。
图像在点M处的切线平行,则点M的坐标为 。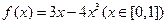 的最大值是 ▲
的最大值是 ▲