题目内容
已知△ABC的两顶点A、C是椭圆
+
=1的二个焦点，顶点B在椭圆上，则
=______．
| x2 |
| 25 |
| y2 |
| 9 |
| sinB |
| sinA+sinC |
由题意可知，A（-4，0），C（4，0），
∵顶点B在椭圆上，∴可以取B（0，3）．此时sinA=sinC=
，sin
=
，cos
=
，sinB=2sin
cos
=2×
×
=
，∴
=
=
．
答案：
．
∵顶点B在椭圆上，∴可以取B（0，3）．此时sinA=sinC=
| 3 |
| 5 |
| B |
| 2 |
| 4 |
| 5 |
| B |
| 2 |
| 3 |
| 5 |
| B |
| 2 |
| B |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| 24 |
| 25 |
| sinB |
| sinA+sinC |
| ||||
|
| 4 |
| 5 |
答案：
| 4 |
| 5 |
练习册系列答案
相关题目
•
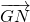的取值范围．
=1的二个焦点，顶点B在椭圆上，则
= ．