题目内容
已知△ABC的两顶点B(-1,0),C(1,0),周长为6(1)求顶点A的轨迹L的方程;
(2)若关于原点对称的两点M,N在曲线L上,且已知G(-4,0),求
| GM |
| GN |
分析:(1)根据三角形的周长和定点,得到点A到两个定点的距离之和等于定值,得到点A的轨迹是椭圆,椭圆的焦点在y轴上,写出椭圆的方程,去掉不合题意的点.
解答:解:(1)∵△ABC的两顶点B(-1,0),C(1,0),周长为6,∴BC=2,AB+AC=4,
∵4>2,∴点A到两个定点的距离之和等于定值,∴点A的轨迹是以B,C为焦点的椭圆,所以椭圆的标准方程是
+
=1(x≠±2)
(2)M,N关于坐标原点对称,设M(x1 ,y1),N(-x1,-y1),
=(x1+4,y1),
=(-x1+4,-y1);
•
=-
-
+16
又
+
=1得
=3-
,∴
•
=-
+13,
∈[0,4),∴
•
∈(12,13].
∵4>2,∴点A到两个定点的距离之和等于定值,∴点A的轨迹是以B,C为焦点的椭圆,所以椭圆的标准方程是
| x2 |
| 4 |
| y2 |
| 3 |
(2)M,N关于坐标原点对称,设M(x1 ,y1),N(-x1,-y1),
| GM |
| GN |
| GM |
| GN |
| x | 2 1 |
| y | 2 1 |
又
| ||
| 4 |
| ||
| 3 |
| y | 2 1 |
| 3 |
| 4 |
| x | 2 1 |
| GM |
| GN |
| 1 |
| 4 |
| x | 2 1 |
| x | 2 1 |
| GM |
| GN |
点评:本题考查椭圆的定义,注意椭圆的定义中要检验两个线段的大小,看能不能构成椭圆,本题是一个易错题,容易忽略掉不合题意的点

练习册系列答案
相关题目
 •
•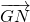 的取值范围.
的取值范围. =1的二个焦点,顶点B在椭圆上,则
=1的二个焦点,顶点B在椭圆上,则 = .
= .