题目内容
已知△ABC的两顶点A、B分别是双曲线2x2-2y2=1的左、右焦点,且sinC是sinA、sinB的等差中项.
(Ⅰ)求顶点C的轨迹T的方程;
(Ⅱ)设P(-2,0),M、N是轨迹T上不同两点,当PM⊥PN时,证明直线MN恒过定点,并求出该定点的坐标.
(Ⅰ)求顶点C的轨迹T的方程;
(Ⅱ)设P(-2,0),M、N是轨迹T上不同两点,当PM⊥PN时,证明直线MN恒过定点,并求出该定点的坐标.
分析:(Ⅰ)由条件可得|BC|+|AC|=2|AB|=4,根据椭圆的定义,即可求得点C的轨迹T的方程;
(Ⅱ)设直线MN的方程,代入椭圆方程,利用韦达定理即PM⊥PN,利用向量知识,即可证得结论.
(Ⅱ)设直线MN的方程,代入椭圆方程,利用韦达定理即PM⊥PN,利用向量知识,即可证得结论.
解答:(Ⅰ)解:由条件知A (-1,0 ),B (1,0 ),且sinA+sinB=2sinC
∴|BC|+|AC|=2|AB|=4 …(2分)
∴点C的轨迹是以A、B为焦点,长轴长2a=4的椭圆(不包括x轴上两点).…(3分)
∴点C的轨迹T的方程是
+
=1 (x≠±2)…(5分)
(Ⅱ)证明:设M (x1,y1)、N (x2,y2),直线MN:x=my+b …(6分)
由
,得 (3m2+4)y2+6mby+3b2-12=0…(7分)
∴y1+y2=-
,y1y2=
∵PM⊥PN,
=(x1+2,y1),
=(x2+2,y2)
∴
•
=( x1+2)(x2+2)+y1y2=(my1+b+2 ) (my2+b+2)+y1y2=0…(9分)
整理,得(m2+1)y1y2+m (b+2)(y1+y2)+(b+2)2=0 …(10分)
∴(m2+1)•
+m (b+2)•(-
)+(b+2)2=0
化简,得7b2+16b+4=0 …(11分)
解得b=-
或b=-2(舍去) …(12分)
故直线MN:x=my-
过定点 (-
,0 ) …(14分)
∴|BC|+|AC|=2|AB|=4 …(2分)
∴点C的轨迹是以A、B为焦点,长轴长2a=4的椭圆(不包括x轴上两点).…(3分)
∴点C的轨迹T的方程是
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)证明:设M (x1,y1)、N (x2,y2),直线MN:x=my+b …(6分)
由
|
∴y1+y2=-
| 6mb |
| 3m2+4 |
| 3b2-12 |
| 3m2+4 |
∵PM⊥PN,
| PM |
| PN |
∴
| PM |
| PN |
整理,得(m2+1)y1y2+m (b+2)(y1+y2)+(b+2)2=0 …(10分)
∴(m2+1)•
| 3b2-12 |
| 3m2+4 |
| 6mb |
| 3m2+4 |
化简,得7b2+16b+4=0 …(11分)
解得b=-
| 2 |
| 7 |
故直线MN:x=my-
| 2 |
| 7 |
| 2 |
| 7 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 •
•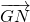 的取值范围.
的取值范围. =1的二个焦点,顶点B在椭圆上,则
=1的二个焦点,顶点B在椭圆上,则 = .
= .