题目内容
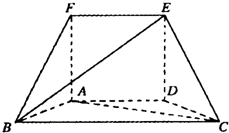 如图,正方形ADEF所在平面和等腰梯形所在平面ABCD垂直,已知BC=2AD=4,∠ABC=60°,BF⊥AC.
如图,正方形ADEF所在平面和等腰梯形所在平面ABCD垂直,已知BC=2AD=4,∠ABC=60°,BF⊥AC.(Ⅰ)求证:AC⊥面ABF;
(Ⅱ)求异面直线BE与AF所成的角;
(Ⅲ) 求该几何体的表面积.
分析:(1)因为面ADEF⊥面ABCD,AF⊥交线AD,AF?面ADEF,所以AF⊥面ABCD由此能够证明AC⊥面ABF.
(2)由(1)得AF,AB,AC两两互相垂直,故可以以A点为坐标原点,建立如图空间直角坐标系A-xyz,则
=(0,2
,0),
=(-3,
,2),
=(0,0,2),由向量法能求出异面直线BE与AC所成的角的余弦值.
(3)由(1)知AF⊥面ABCD,所以AF⊥AB,又AB=BCcos60°=2,所以△ABF的面积S1=
|AF|•|AB|=2.同理△CDE的面积S2=2,等腰梯形BCEF的上底长为2,下底长为4,两腰长均为2
,则它的高为
,等腰梯形ABCD的上底长为2,下底长为4,两腰长均为2,它的高为
,由此能求出该几何体的表面积.
(2)由(1)得AF,AB,AC两两互相垂直,故可以以A点为坐标原点,建立如图空间直角坐标系A-xyz,则
| AC |
| 3 |
| BE |
| 3 |
| AF |
(3)由(1)知AF⊥面ABCD,所以AF⊥AB,又AB=BCcos60°=2,所以△ABF的面积S1=
| 1 |
| 2 |
| 2 |
| 7 |
| 3 |
解答: (1)证明:因为面ADEF⊥面ABCD,AF⊥交线AD,AF?面ADEF,
(1)证明:因为面ADEF⊥面ABCD,AF⊥交线AD,AF?面ADEF,
所以AF⊥面ABCD.(2分)
故 AF⊥AC,又 BF⊥AC,AF∩BF=F.
所以AC⊥面ABF.…(4分)
(2)解:由(1)得AF,AB,AC两两互相垂直,
故可以以A点为坐标原点,
建立如图空间直角坐标系A-xyz,
∵BC=2AD=4,∠ABC=60°,BF⊥AC.
∴A(0,0,0),B(2,0,0),C(0,2
,0),E(-1,
,2),F(0,0,2).…(6分)
=(0,2
,0),
=(-3,
,2),
=(0,0,2),
cos<
,
>=
=
=
.
即异面直线BE与AF所成的角的余弦值为
.…(8分)
(3)解:由(1)知AF⊥面ABCD,所以AF⊥AB,又AB=BCcos60°=2,
所以△ABF的面积S1=
|AF|•|AB|=2.…(9分)
同理△CDE的面积S2=2,等腰梯形BCEF的上底长为2,下底长为4,两腰长均为2
,则它的高为
,
所以其面积S3=
×(2+4)×
=3
.…(10分)
等腰梯形ABCD的上底长为2,下底长为4,两腰长均为2,
则它的高为
,
所以其面积S4=
×(2+4)×
=3
.…(11分)
故该几何体的表面积S=S1+S2+S3+S4+4=3
+3
+8.…(12分)
 (1)证明:因为面ADEF⊥面ABCD,AF⊥交线AD,AF?面ADEF,
(1)证明:因为面ADEF⊥面ABCD,AF⊥交线AD,AF?面ADEF,所以AF⊥面ABCD.(2分)
故 AF⊥AC,又 BF⊥AC,AF∩BF=F.
所以AC⊥面ABF.…(4分)
(2)解:由(1)得AF,AB,AC两两互相垂直,
故可以以A点为坐标原点,
建立如图空间直角坐标系A-xyz,
∵BC=2AD=4,∠ABC=60°,BF⊥AC.
∴A(0,0,0),B(2,0,0),C(0,2
| 3 |
| 3 |
| AC |
| 3 |
| BE |
| 3 |
| AF |
cos<
| AF |
| BE |
| ||||
|
|
| 4 |
| 2×4 |
| 1 |
| 2 |
即异面直线BE与AF所成的角的余弦值为
| 1 |
| 2 |
(3)解:由(1)知AF⊥面ABCD,所以AF⊥AB,又AB=BCcos60°=2,
所以△ABF的面积S1=
| 1 |
| 2 |
同理△CDE的面积S2=2,等腰梯形BCEF的上底长为2,下底长为4,两腰长均为2
| 2 |
| 7 |
所以其面积S3=
| 1 |
| 2 |
| 7 |
| 7 |
等腰梯形ABCD的上底长为2,下底长为4,两腰长均为2,
则它的高为
| 3 |
所以其面积S4=
| 1 |
| 2 |
| 3 |
| 3 |
故该几何体的表面积S=S1+S2+S3+S4+4=3
| 3 |
| 7 |
点评:本题考查AC⊥面ABF的证明,求异面直线BE与AF所成的角,求该几何体的表面积.解题时要认真审题,合理地化空间几何问题为平面几何问题,注意向量法的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
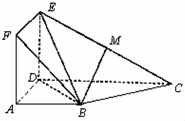 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.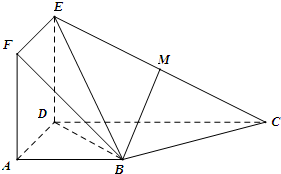 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.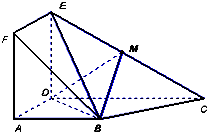 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD, 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4.