题目内容
19.矩形ABCD中,AD=2,AB=4,E,F分别为边AB,AD的中点,将△ADE沿DE折起,点A,F折起后分别为点A′,F′,得到四棱锥A′-BCDE.给出下列几个结论:①A′,B,C,F′四点共面;
②EF'∥平面A′BC;
③若平面A′DE⊥平面BCDE,则CE⊥A′D;
④四棱锥A′-BCDE体积的最大值为$\sqrt{2}$.
其中正确的是②③(填上所有正确的序号).
分析 根据折叠前后图形的特点逐个分析即可.
解答 解:由题意知,矩形ABCD折叠后的图 由图可知,F'点不在平面A'BC上,因此四点不共面,①说法错误;去A'C中点为G,连接F'G,GB,F'E如图
由图可知,F'点不在平面A'BC上,因此四点不共面,①说法错误;去A'C中点为G,连接F'G,GB,F'E如图 所以F'G为三角形A'DC的中位线,∵DC=2EB=2F'G∴F'G平行且等于EB,四边形F'EBG是平行四边形,∴EF'∥GB,GB?面A'BC,②正确;∵AB=2AD,∴DE⊥CE,DE为垂线,由面面垂直结论,CE⊥面A'DE,③正确;当面A'DE旋转到与底面垂直时体积最大,为2$\sqrt{2}$.
所以F'G为三角形A'DC的中位线,∵DC=2EB=2F'G∴F'G平行且等于EB,四边形F'EBG是平行四边形,∴EF'∥GB,GB?面A'BC,②正确;∵AB=2AD,∴DE⊥CE,DE为垂线,由面面垂直结论,CE⊥面A'DE,③正确;当面A'DE旋转到与底面垂直时体积最大,为2$\sqrt{2}$.
故答案为:②③.
点评 该题主要考察了空间四棱锥线与面的位置关系,以及线面平行,面面垂直定理的应用,涉及计算,属于易错题.

练习册系列答案
相关题目
4.下面四个命题:
(1)“2a>2b”是“lna>lnb”的充要条件.
(2)命题“正方形是矩形”的否定是“正方形不是矩形”.
(3)“直线a∥直线b”的充分不必要条件是“直线a平行于直线b所在的平面”.
(4)命题“若x≤$\frac{4}{3}$,则$\frac{1}{x-1}$≥3”的逆命题是真命题.
其中正确命题的序号是( )
(1)“2a>2b”是“lna>lnb”的充要条件.
(2)命题“正方形是矩形”的否定是“正方形不是矩形”.
(3)“直线a∥直线b”的充分不必要条件是“直线a平行于直线b所在的平面”.
(4)命题“若x≤$\frac{4}{3}$,则$\frac{1}{x-1}$≥3”的逆命题是真命题.
其中正确命题的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (4) | D. | (2)(4) |
8.执行如图的程序框图,则输出S的值为( )


| A. | 2016 | B. | 2 | C. | $\frac{1}{2}$ | D. | -1 |
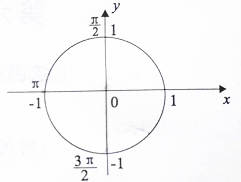 单位圆上三角函数值的集合解释是“角在弧上,值在线上”,试在图中画出α属于第Ⅲ象限的一个正弦值,余弦值.
单位圆上三角函数值的集合解释是“角在弧上,值在线上”,试在图中画出α属于第Ⅲ象限的一个正弦值,余弦值. 某班有60人,在三月份的月考中该班数学成绩统计得到如下频率分布直方图(满分150分,90分为及格,120分以上为优秀,且最低分数是75分).如图设第一个小矩形的高为h,各小矩形的高如图所示:
某班有60人,在三月份的月考中该班数学成绩统计得到如下频率分布直方图(满分150分,90分为及格,120分以上为优秀,且最低分数是75分).如图设第一个小矩形的高为h,各小矩形的高如图所示: