题目内容
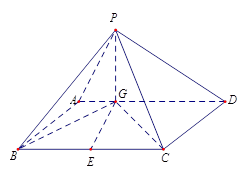
如图,已知六棱锥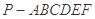 的底面是正六边形,
的底面是正六边形,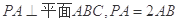 则下列结论正确的是( )
则下列结论正确的是( )
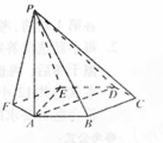
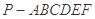 的底面是正六边形,
的底面是正六边形,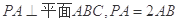 则下列结论正确的是( )
则下列结论正确的是( )
A.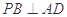 |
B.  |
C.直线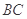 ∥ ∥ |
D.直线 所成的角为45° 所成的角为45° |
D
试题分析:选D.∵AD与PB在平面的射影AB不垂直,∴A不成立;又平面PAB⊥平面PAE,∴

 也不成立;BC∥AD∥平面PAD, ∴直线
也不成立;BC∥AD∥平面PAD, ∴直线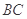 ∥
∥ 也不成立。在
也不成立。在 中,PA=AD=2AB,∴∠PDA=45°. ∴D正确.
中,PA=AD=2AB,∴∠PDA=45°. ∴D正确.
练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
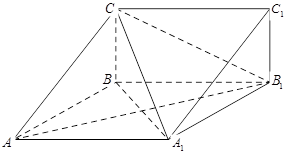
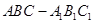 中,四边形
中,四边形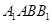 为菱形,
为菱形,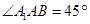 ,四边形
,四边形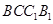 为矩形,若
为矩形,若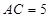 ,
,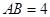 ,
,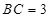 .
.
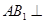 面
面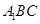 ;
;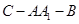 的余弦值;
的余弦值;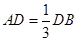 ,点C为圆O上一点,且
,点C为圆O上一点,且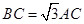 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.
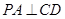 ;
;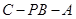 的余弦值.
的余弦值.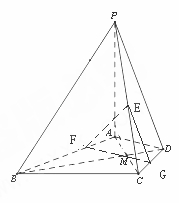
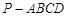 中,底面
中,底面 是平行四边形,
是平行四边形,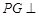 平面
平面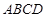 ,垂足为
,垂足为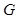 ,
,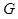 在
在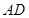 上且
上且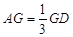 ,
,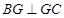 ,
,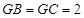 ,
,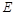 是
是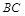 的中点,四面体
的中点,四面体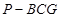 的体积为
的体积为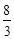 .
.
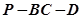 的正切值;
的正切值;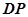 到平面
到平面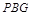 所成角的正弦值;
所成角的正弦值;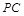 上是否存在一点
上是否存在一点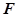 ,使异面直线
,使异面直线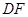 与
与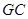 所成的角为
所成的角为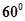 ,若存在,确定点
,若存在,确定点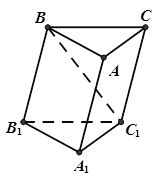
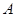 作平面
作平面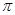 的垂线,垂足为
的垂线,垂足为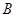 ,记
,记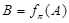 .设
.设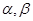 是两个不同的平面,对空间任意一点
是两个不同的平面,对空间任意一点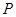 ,
,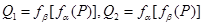 ,恒有
,恒有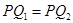 ,则( )
,则( )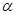 与平面
与平面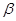 垂直
垂直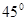
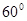
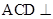 平面BCD(如图2),则下列结论中不正确的是( )
平面BCD(如图2),则下列结论中不正确的是( )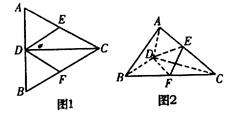
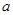 、
、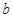 是两条不同直线,
是两条不同直线,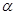 、
、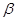 是两个不同平面,则下列命题错误的是( )
是两个不同平面,则下列命题错误的是( )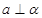 ,
,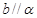 ,则
,则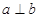
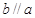 ,
,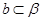 ,则
,则
 ,
,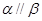 ,则
,则
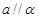 ,
,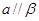 ,则
,则