题目内容
已知函数f(x)=|x-2|-|x-5|.
(1)证明:-3≤f(x)≤3;
(2)求不等式f(x)≥x2-8x+15的解集.
(1)f(x)=|x-2|-|x-5|
=
当2<x<5时,-3<2x-7<3.
所以-3≤f(x)≤3.
(2)由(1)可知,
当x≤2时,f(x)≥x2-8x+15的解集为空集;
当2<x<5时,f(x)≥x2-8x+15的解集为{x|5- ≤x<5};
≤x<5};
当x≥5时,f(x)≥x2-8x+15的解集为{x|5≤x≤6}.
综上,不等式f(x)≥x2-8x+15的解集为{x|5- ≤x≤6}.
≤x≤6}.

练习册系列答案
相关题目
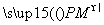 ·
·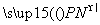 =0,则点P的轨迹方程为( )
=0,则点P的轨迹方程为( )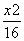 +y2=1 B.x2+y2=4
+y2=1 B.x2+y2=4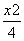 -
- =1上一点P到它的右焦点的距离是8,那么点P到它的左焦点的距离是( )
=1上一点P到它的右焦点的距离是8,那么点P到它的左焦点的距离是( )