题目内容
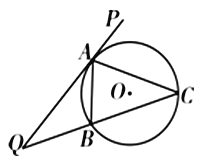
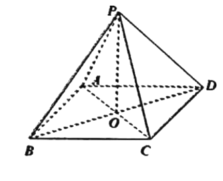
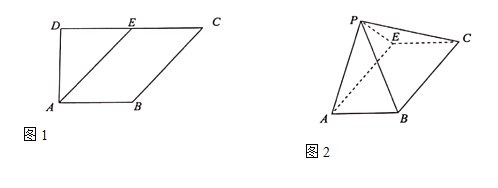
【题目】如图甲，E是边长等于2的正方形的边CD的中点，以AE、BE为折痕将△ADE与△BCE折起，使D，C重合(仍记为D)，如图乙.
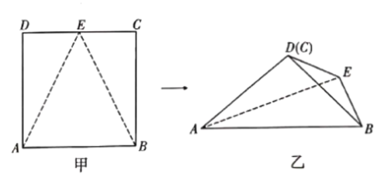
（1）探索:折叠形成的几何体中直线DE的几何性质(写出一条即可，不含DE⊥DA，DE⊥DB，说明理由)；
（2）求二面角D-BE-A的余弦值
【答案】（1）几何性质见解析，理由见解析；（2）
【解析】
（1）根据折前折后折痕同侧的位置关系、长度不变，可以证明
平面
，据此结论也可得到
，或
与平面内任一直线都垂直，也可计算直线与平面
所成角等于
；
（2）建立空间直角坐标系，利用向量法可求二面角的余弦值.
（1）性质1：平面.
证明如下：翻折前，
，
翻折后仍然
，
且
，
则平面.
性质2：.
证明如下：
与性质1证明方法相同，得到平面.
又因
平面，则.
性质3：与平面内任一直线都垂直.
证明如下：
与性质1证明方法相同，得到平面，
从而与平面内任一直线都垂直.
性质4：直线与平面所成角等于.
证明如下：
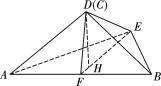
如图，取
的中点
，连接
，
，
由
得
，
与性质2证明相同，得，
再因
，则
平面
，进而平面
平面.
作
于
，则
平面，
即
就是直线与平面所成的角.
，
，
，
.
（2）与（1）之性质4证明相同，得到
，平面，
，平面内，则平面平面.
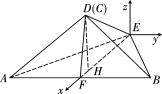
以
为坐标原点、为
轴建立如图所示的空间直角坐标系.
，
，
，则平面的一个法向量
，
，
，
，
.
设
是平面
的法向量，
则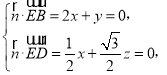
取
，求得一个法向量
记二面角
的大小为
，则与
相等或互补，
，
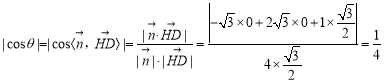因是锐角，则
.
练习册系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
