题目内容
4.已知函数$f(x)=\sqrt{3}{cos^2}x+sinxcosx$,(1)若$f(a)=\frac{{1+\sqrt{3}}}{2}$,求a;
(2)如果关于x的方程|f(x)|=m在区间(0,π)上有两个不同的实根,求实数m的取值范围.
分析 (1)利用二倍角公式、两角和的正弦函数公式化简函数为一个角的一个三角函数的形式,利用正弦图象,求α;
(2)如果关于x的方程|f(x)|=m,在区间(0,π)上有两个不同的实根,求实数m的取值范围.
解答 解:(1)解:y=$\sqrt{3}$cos2x+sinxcosx
=$\sqrt{3}$×$\frac{1+cos2x}{2}$+$\frac{1}{2}sin2x$=$\frac{1}{2}sin2x+\frac{\sqrt{3}}{2}cos2x+\frac{\sqrt{3}}{2}$
=$six(2x+\frac{π}{3})+\frac{\sqrt{3}}{2}$,
∵$f(a)=\frac{{1+\sqrt{3}}}{2}$,∴sin(2α+$\frac{π}{3}$)=$\frac{1}{2}$,解得2$α+\frac{π}{3}$=2k$π+\frac{π}{6}$或2$α+\frac{π}{3}$=2kπ+$\frac{5π}{6}$,
$α=kπ-\frac{π}{12}$或$α=kπ+\frac{π}{4}$ (k∈Z).
(2)画出y=|f(x)|的图象,再画出y=m的图象,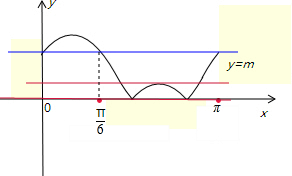
结合图象可知它们有两个不同的交点的情况;
可得m=0,1-$\frac{\sqrt{3}}{2}$<m<$\sqrt{3}$,$\sqrt{3}$<m<1+$\frac{\sqrt{3}}{2}$.
点评 本题考查三角函数式的化简求值,二倍角公式、两角和的正弦函数公式的应用,考查函数与方程的思想,数形结合思想,考查计算能力,属于中档题.

练习册系列答案
相关题目
14.设集合A={x|x<2},则( )
| A. | ∅∈A | B. | $\sqrt{3}∉A$ | C. | $\sqrt{3}∈A$ | D. | $\sqrt{3}$$\underset{?}{≠}$A |