题目内容
设z1是方程x2-6x+25=0的一个根.
(1)求z1;
(2)设z2=a+i(其中i为虚数单位,a∈R),若z2的共轭复数
满足|
•
|=125
,求
.
(1)求z1;
(2)设z2=a+i(其中i为虚数单位,a∈R),若z2的共轭复数
. |
| z2 |
| z | 3 1 |
. |
| z2 |
| 5 |
| z | 2 2 |
分析:(1)直接利用实系数一元二次方程的求根公式求解;
(2)由z2=a+i得其共轭复数,把z1及
代入|
•
|=125
,整理后求解a的值,代入z2=a+i后求解
.
(2)由z2=a+i得其共轭复数,把z1及
. |
| z2 |
| z | 3 1 |
. |
| z2 |
| 5 |
| z | 2 2 |
解答:解 (1)∵△=62-4×25=-64,
∴x=
=3±4i,即z1=3-4i或z1=3+4i;
(2)由z2=a+i,得
=a-i.
当z1=3-4i时,
则|z13•
|=|(3-4i)3•(a-i)|=125
,得
|(-117-44i)(a-i)|=125
,
整理得:125
=125
,∴a=±2.
当z1=3+4i时,
则|z13•
|=|(3+4i)3•(a-i)|=125
,得
|(-117+44i)(a-i)|=125
,
整理得:125
=125
,∴a=±2.
综上:
当a=-2时,
=(-2+i)2=3-4i;
当a=2时,
=(2+i)2=3+4i.
∴x=
6±
| ||
| 2 |
(2)由z2=a+i,得
. |
| z2 |
当z1=3-4i时,
则|z13•
. |
| z2 |
| 5 |
|(-117-44i)(a-i)|=125
| 5 |
整理得:125
| a2+1 |
| 5 |
当z1=3+4i时,
则|z13•
. |
| z2 |
| 5 |
|(-117+44i)(a-i)|=125
| 5 |
整理得:125
| a2+1 |
| 5 |
综上:
当a=-2时,
| z | 2 2 |
当a=2时,
| z | 2 2 |
点评:本题考查了复数代数形式的乘除运算,训练了实系数一元二次方程虚根的求法,考查了复数模的求法,考查了学生的计算能力,是基础题.

练习册系列答案
相关题目

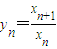 ,
,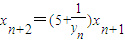 .n∈N*.
.n∈N*.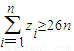 ;
;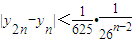 .
.