题目内容
已知:x1,x2(x1<x2)是方程x2-6x+5=0的两根,且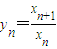 ,
,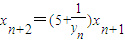 .n∈N*.
.n∈N*.(1)求y1,y2,y3的值;
(2)设zn=ynyn+1,求证:
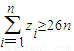 ;
;(3)求证:对?n∈[2,+∞)有
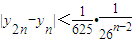 .
.
【答案】分析:(1)先根据方程的根求出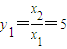 ,再根据yn的表达式和xn+2关于xn+1表达式,分别取n=1、2、3即可求出;
,再根据yn的表达式和xn+2关于xn+1表达式,分别取n=1、2、3即可求出;
(2)根据xn、yn各项为正的特征,求出z1=y1y2=26,再根据zn的表达式及不等式的性质可得zn>26(n≥2),最后代入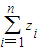 ,命题得证;
,命题得证;
(3)求出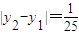
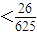 ,再通过yn+1关于yn的表达式,证出
,再通过yn+1关于yn的表达式,证出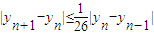 ,利用数列的递推特性进一步证出|yn+1-yn|≤
,利用数列的递推特性进一步证出|yn+1-yn|≤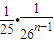 ,最后用绝对值不等式的性质将|y2n-yn|分解为不小于它本身的和:|yn+1-yn|+…+|y2n-1-y2n-2|+|y2n-y2n-1|的形式,得出等比数列求和表达式,再将所得结果适当放大,使命题得证.
,最后用绝对值不等式的性质将|y2n-yn|分解为不小于它本身的和:|yn+1-yn|+…+|y2n-1-y2n-2|+|y2n-y2n-1|的形式,得出等比数列求和表达式,再将所得结果适当放大,使命题得证.
解答:解:(1)解方程x2-6x+5=0 得x1=1,x2=5,---------------------------------------------1分
∴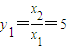 ,------------------------------------------------------------------------------2分
,------------------------------------------------------------------------------2分 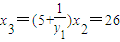 ,
,
∴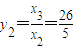 ,--------------------------------------------------------------------------3分
,--------------------------------------------------------------------------3分 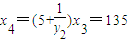 ,
,
∴ --------------------------------------------4分
--------------------------------------------4分
(2)由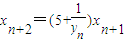 得
得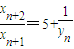 即
即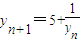 ⇒yn+1yn=5yn+1----------------------6分
⇒yn+1yn=5yn+1----------------------6分
当n≥2 时yn>5,于是z1=y1y2=26,zn=ynyn+1=5yn+1>26 (n≥2 )
∴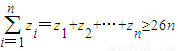 --------------------------------------------------------------------9分
--------------------------------------------------------------------9分
(3)当n≥2 时,有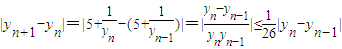
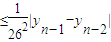
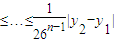 =
=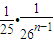 ----------------------------------------12分
----------------------------------------12分
∵|y2n-yn|=|y2n-y2n-1+y2n-1-y2n-2+y2n-2-…+yn+1-yn|
∴|y2n-yn|≤|yn+1-yn|+…+|y2n-1-y2n-2|+|y2n-y2n-1|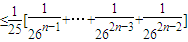 =
=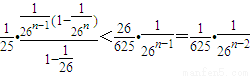
∴对?n∈N* 有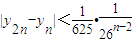 (n∈N*)----------------------------------------------14分
(n∈N*)----------------------------------------------14分
点评:把握数列的递推关系是解决前两个问题的关键,第三问用到数列递推在不等式中的应用,证明不等式用到绝对值不等式的性质以及不等式放缩的技巧,再与数列的求和相结合,是数列与不等式两个知识点的完美交汇.
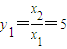 ,再根据yn的表达式和xn+2关于xn+1表达式,分别取n=1、2、3即可求出;
,再根据yn的表达式和xn+2关于xn+1表达式,分别取n=1、2、3即可求出;(2)根据xn、yn各项为正的特征,求出z1=y1y2=26,再根据zn的表达式及不等式的性质可得zn>26(n≥2),最后代入
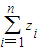 ,命题得证;
,命题得证;(3)求出
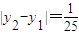
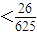 ,再通过yn+1关于yn的表达式,证出
,再通过yn+1关于yn的表达式,证出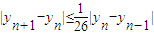 ,利用数列的递推特性进一步证出|yn+1-yn|≤
,利用数列的递推特性进一步证出|yn+1-yn|≤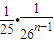 ,最后用绝对值不等式的性质将|y2n-yn|分解为不小于它本身的和:|yn+1-yn|+…+|y2n-1-y2n-2|+|y2n-y2n-1|的形式,得出等比数列求和表达式,再将所得结果适当放大,使命题得证.
,最后用绝对值不等式的性质将|y2n-yn|分解为不小于它本身的和:|yn+1-yn|+…+|y2n-1-y2n-2|+|y2n-y2n-1|的形式,得出等比数列求和表达式,再将所得结果适当放大,使命题得证.解答:解:(1)解方程x2-6x+5=0 得x1=1,x2=5,---------------------------------------------1分
∴
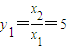 ,------------------------------------------------------------------------------2分
,------------------------------------------------------------------------------2分 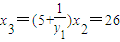 ,
,∴
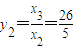 ,--------------------------------------------------------------------------3分
,--------------------------------------------------------------------------3分 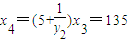 ,
,∴
 --------------------------------------------4分
--------------------------------------------4分(2)由
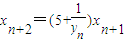 得
得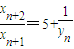 即
即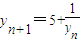 ⇒yn+1yn=5yn+1----------------------6分
⇒yn+1yn=5yn+1----------------------6分当n≥2 时yn>5,于是z1=y1y2=26,zn=ynyn+1=5yn+1>26 (n≥2 )
∴
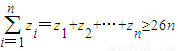 --------------------------------------------------------------------9分
--------------------------------------------------------------------9分(3)当n≥2 时,有
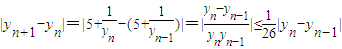
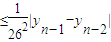
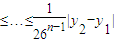 =
=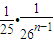 ----------------------------------------12分
----------------------------------------12分∵|y2n-yn|=|y2n-y2n-1+y2n-1-y2n-2+y2n-2-…+yn+1-yn|
∴|y2n-yn|≤|yn+1-yn|+…+|y2n-1-y2n-2|+|y2n-y2n-1|
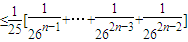 =
=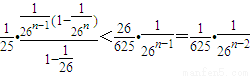
∴对?n∈N* 有
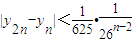 (n∈N*)----------------------------------------------14分
(n∈N*)----------------------------------------------14分点评:把握数列的递推关系是解决前两个问题的关键,第三问用到数列递推在不等式中的应用,证明不等式用到绝对值不等式的性质以及不等式放缩的技巧,再与数列的求和相结合,是数列与不等式两个知识点的完美交汇.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目