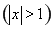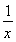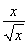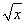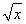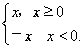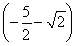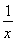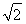Question

求下列各题中的函数f(x)的解析式．

(1) 已知f(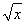＋2)＝x＋4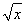，求f(x)；

(2) 已知f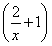＝lgx，求f(x)；

(3) 已知函数y＝f(x)满足2f(x)＋f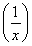＝2x，x∈R且x≠0，求f(x)；

(4) 已知f(x)是二次函数，且满足f(0)＝1，f(x＋1)＝f(x)＋2x，求f(x)．

 

Answer 1

（1）f(x)＝x2－4(x≥2)（2）f(x)＝lg(x>1)．（3）f(x)＝x－（4）f(x)＝x2－x＋1.

【解析】(1) (解法1)设t＝＋2，则＝t－2，即x＝(t－2)2，

∴ f(t)＝(t－2)2＋4(t－2)＝t2－4，

∴ f(x)＝x2－4(x≥2)．

(解法2)∵ f(＋2)＝(＋2)2－4，∴ f(x)＝x2－4(x≥2)．

(2) 设t＝＋1，则x＝，∴ f(t)＝lg，即f(x)＝lg(x>1)．

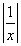
(3) 由2f(x)＋f＝2x，①将x换成，则换成x，得2f＋f＝，②

①×2－②，得3f(x)＝4x－，得f(x)＝x－.

(4) ∵ f(x)是二次函数，∴ 设f(x)＝ax2＋bx＋c(a≠0)．由f(0)＝1，得c＝1.

由f(x＋1)＝f(x)＋2x，得a(x＋1)2＋b(x＋1)＋1＝(ax2＋bx＋1)＋2x，

整理，得(2a－2)x＋(a＋b)＝0，由恒等式原理，知

∴f(x)＝x2－x＋1