题目内容
函数y=x3-ax2+4在（0，2）内单调递减，求实数a的取值范围．
考点：利用导数研究函数的单调性,函数单调性的性质
专题：导数的综合应用
分析：求出导函数，令导函数小于等于0在（0，2）内恒成立，分离出参数a，求出函数的范围，得到a的范围．
解答：
解：∵函数f（x）=x3-ax2+4在（0，2）内单调递减，
∴f′（x）=3x2-2ax≤0在（0，2）内恒成立，
即 a≥
x在（0，2）内恒成立，
∵
x＜3
∴a≥3，
实数a的取值范围：[3，+∞）．
∴f′（x）=3x2-2ax≤0在（0，2）内恒成立，
即 a≥
| 3 |
| 2 |
∵
| 3 |
| 2 |
∴a≥3，
实数a的取值范围：[3，+∞）．
点评：本题考查函数在区间上的单调性已知求参数的范围的问题，递增时，令导函数大于等于0恒成立；递减时，令导数小于等于0恒成立．
练习册系列答案
阅读快车系列答案
相关题目
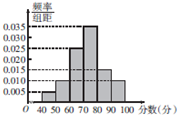某校学生在一次学业水平测试中的数学成绩制成如图所示的频率分布直方图，60分以下的人要补考，已知90分以上的有80人，则该校需要补考的人数为（ ）| A、120 | B、150 |
| C、180 | D、200 |
设a2-a＞0，函数y=a|x|（a＞0，a≠1）的图象形状大致是（ ）
A、 |
B、 |
C、 |
D、 |
若π＜α＜
，则
+
的化简结果（ ）
| 3π |
| 2 |
|
|
A、
| ||
B、-
| ||
C、
| ||
D、-
|
方程x2+3x-3=0的解在区间（ ）
| A、（0，1）内 |
| B、（1，2）内 |
| C、（2，3）内 |
| D、以上均不对 |
已知（x，y）满足不等式
，z=x+ay，当且仅当在点（2，2）取得最大值，则实数a的取值范围是（ ）
|
A、（-∞，-
| ||||
B、（-
| ||||
C、（-
| ||||
D、（-
|