题目内容
已知椭圆的的右顶点为A,离心率![]() ,过左焦点
,过左焦点![]() 作直线
作直线![]() 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线![]() 交于点
交于点![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)证明以线段![]() 为直径的圆经过焦点
为直径的圆经过焦点![]() .
.
(Ⅰ)解: 由已知 ![]()
∴ ![]() ,
,
∴ 椭圆方程为![]() .——————————————5分
.——————————————5分
(Ⅱ) 设直线![]() 方程为
方程为 ![]() ,
,
由 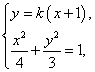 得
得![]() .
.
设![]() ,则
,则![]() .—————7分
.—————7分
设![]() ,则由
,则由![]() 共线,
共线,![]() 得
得
![]() 有
有 ![]() .同理
.同理 ![]() .
.
∴ 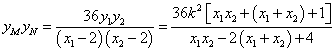 .——————9分
.——————9分
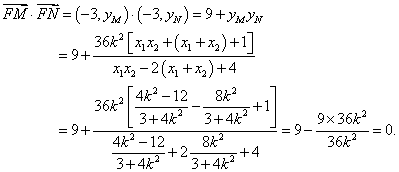
∴![]() ,即
,即![]() ,以线段
,以线段![]() 为直径的圆经过点F;————12分
为直径的圆经过点F;————12分
当直线![]() 的斜率不存在时,不妨设
的斜率不存在时,不妨设![]() .则有
.则有
![]() ,
,
∴ ![]() ,即
,即![]() ,以线段
,以线段![]() 为直径的圆经过点F.
为直径的圆经过点F.
综上所述,以线段![]() 为直径的圆经过定点F. ———————————14分
为直径的圆经过定点F. ———————————14分

练习册系列答案
相关题目
 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
. ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
. ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
.