题目内容
本小题共14分)
已知椭圆的的右顶点为A,离心率 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)证明以线段 为直径的圆经过焦点
为直径的圆经过焦点 .
.
【答案】
(Ⅰ)解: 由已知 
∴  ,
,
∴ 椭圆方程为 .——————————————5分
.——————————————5分
(Ⅱ)
设直线 方程为
方程为  ,
,
由  得
得 .
.
设 ,则
,则 .—————7分
.—————7分
设 ,则由
,则由 共线,得
共线,得
 有
有  .同理
.同理  .
.
∴  .——————9分
.——————9分

∴ ,即
,即 ,以线段
,以线段 为直径的圆经过点F;————12分
为直径的圆经过点F;————12分
当直线 的斜率不存在时,不妨设
的斜率不存在时,不妨设 .则有
.则有
 ,
,
∴  ,即
,即 ,以线段
,以线段 为直径的圆经过点F.
为直径的圆经过点F.
综上所述,以线段 为直径的圆经过定点F. ———————————14分
为直径的圆经过定点F. ———————————14分
【解析】略

练习册系列答案
相关题目
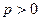 ,动点
,动点 到定点
到定点
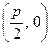 的距离比
的距离比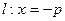 的距离小
的距离小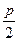 .
. 的方程;
的方程; 是轨迹
是轨迹 的两个不同点,
的两个不同点,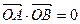 ,求
,求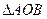 面积的最小值;
面积的最小值;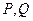 关于直线
关于直线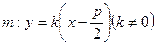 对称?若存在,求出直线
对称?若存在,求出直线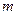 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.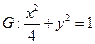 .过点(m,0)作圆
.过点(m,0)作圆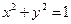 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点.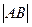 表示为m的函数,并求
表示为m的函数,并求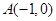 ,
,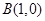 ,动点P满足
,动点P满足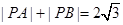 ,记动点P的轨迹为W.
,记动点P的轨迹为W.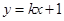 与曲线W交于不同的两点C,D,若存在点
与曲线W交于不同的两点C,D,若存在点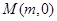 ,使得
,使得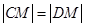 成立,求实数m的取值范围.
成立,求实数m的取值范围.