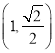题目内容
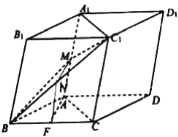
【题目】如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
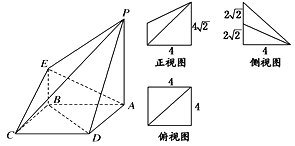
(1)求四棱锥P-ABCD的体积;
(2)证明:BD∥平面PEC;
(3)线段BC上是否存在点M,使得AE⊥PM?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】
(1)结合三视图,得到四棱锥P﹣ABCD的相关棱长,从而求出体积;(2)连接AC交BD于O点,取PC中点F,连接OF,要证明BD∥平面PEC,只需证明BD平行平面PEC内的直线EF即可;(3)连接BP,要证AE⊥PM,只需证明AE⊥平面PBM,即可证明AE⊥PM.
(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥平面ABCD,PA∥EB,
且PA=4![]() ,BE=2
,BE=2![]() ,AB=AD=CD=CB=4,∴VP﹣ABCD=
,AB=AD=CD=CB=4,∴VP﹣ABCD=![]() PA×SABCD=
PA×SABCD=![]() ×4
×4![]() ×4×4=
×4×4=![]() .
.
(2)证明:连接AC交BD于O点,取PC中点F,连接OF,∵EB∥PA,且EB=![]() PA,
PA,
又OF∥PA,且OF=![]() PA,∴EB∥OF,且EB=OF,∴四边形EBOF为平行四边形,
PA,∴EB∥OF,且EB=OF,∴四边形EBOF为平行四边形,
∴EF∥BD.又EF平面PEC,BD平面PEC,所以BD∥平面PEC.
(3)连接BP,∵![]() =
=![]() =
=![]() ,∠EBA=∠BAP=90°,
,∠EBA=∠BAP=90°,
∴△EBA∽△BAP,∴∠PBA=∠BEA,∴∠PBA+∠BAE=∠BEA+∠BAE=90°,
∴PB⊥AE.又∵BC⊥平面APEB,∴BC⊥AE,且PB![]() BC=B
BC=B
∴AE⊥平面PBC,点M在线段BC上∴AE⊥PM.

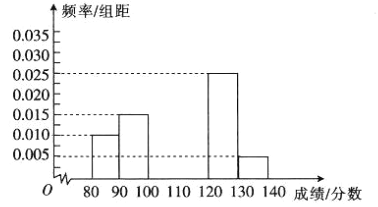
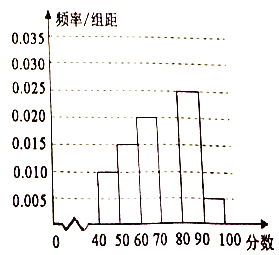
【题目】据统计,仅在北京地区每天就有500万单快递等待派送,近5万多名快递员奔跑在一线,快递网点人员流动性也较强,各快递公司需要经常招聘快递员,保证业务的正常开展.下面是50天内甲、乙两家快递公司的快递员每天送货单数统计表:
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 6 | 14 | 24 | 6 | |
已知这两家快递公司的快递员日工资方案分别为:甲公司规定底薪![]() 元,每单抽成
元,每单抽成![]() 元;乙公司规定底薪
元;乙公司规定底薪![]() 元,每日前
元,每日前![]() 单无抽成,超过
单无抽成,超过![]() 单的部分每单抽成
单的部分每单抽成![]() 元.
元.
(1)分别求甲、乙快递公司的快递员的日工资![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
(2)小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作,如果仅从日收入的角度考虑,以这50天的送货单数为样本,将频率视为概率,请你利用所学的统计学知识为他作出选择,并说明理由.