题目内容
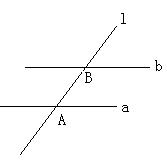
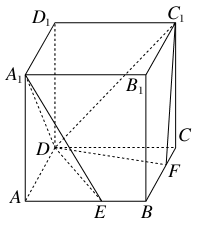
如图,在四棱锥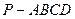 中,底面
中,底面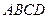 是矩形,
是矩形,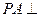 平面
平面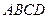 ,且
,且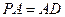 ,点
,点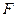 是棱
是棱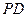 的中点,点
的中点,点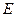 在棱
在棱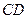 上移动.
上移动.
(Ⅰ)当点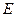 为
为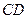 的中点时,试判断直线
的中点时,试判断直线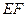 与平面
与平面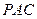 的关系,并说明理由;
的关系,并说明理由;
(Ⅱ)求证: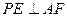 .
.
解:(Ⅰ)当点 为CD的中点时,
为CD的中点时, 平面PAC. 理
平面PAC. 理 由如下:
由如下: 点
点 分别为
分别为 ,
, 的中点,
的中点,
 .
. 
 ,
, ,
,
 平面PAC.
平面PAC.
(Ⅱ)

 ,
, ,
,  .
.
又 是矩形,
是矩形, ,
, ,
, .
.
 .
.
 ,点
,点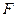 是
是 的中点,
的中点,  .
.
又 ,
,  .
. 
 .
. 
解析

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
△ABC的顶点分别为A(1,-1,2),B(5,-6,2),C(1,3,-1)则AC边上的高BD等于( )
| A.2 |
B.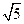 |
| C.5 |
| D.6 |
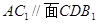 ;
;
 中,设
中,设 ,
, ,
, 上存在点
上存在点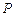 满足
满足
 平面
平面 ,求实数
,求实数 的取值范围
的取值范围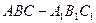 中,底面
中,底面 是边长为2的正三角形,侧棱长为3,且侧棱
是边长为2的正三角形,侧棱长为3,且侧棱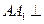 面
面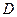 是
是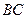 的中点.
的中点.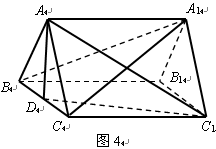
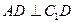 ;
;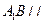 平面
平面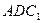 .
.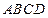 中,
中, ,
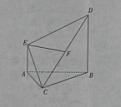
,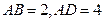 将
将 沿
沿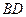 折起到
折起到 的位置,使平面
的位置,使平面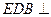 平面
平面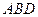
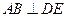 (Ⅱ)求三棱锥
(Ⅱ)求三棱锥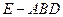 的侧面积。
的侧面积。
 ,求证:
,求证: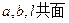 .
.
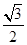 B.
B.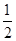 C.
C. D.
D.