题目内容
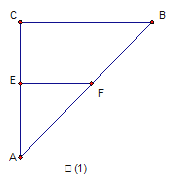
(本小题满分12分)如图(1),△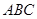 是等腰直角三角形,
是等腰直角三角形,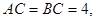
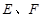 分别为
分别为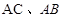 的中点,将△
的中点,将△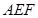 沿
沿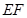 折起,使
折起,使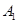 在平面
在平面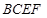 上的射影
上的射影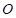 恰好为
恰好为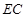 的中点,得到图(2)。
的中点,得到图(2)。
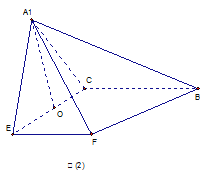
(Ⅰ)求证: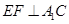 ;(Ⅱ)求三棱锥
;(Ⅱ)求三棱锥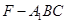 的体积。
的体积。
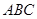 是等腰直角三角形,
是等腰直角三角形,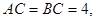
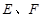 分别为
分别为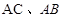 的中点,将△
的中点,将△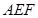 沿
沿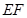 折起,使
折起,使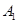 在平面
在平面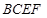 上的射影
上的射影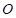 恰好为
恰好为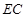 的中点,得到图(2)。
的中点,得到图(2)。

(Ⅰ)求证:
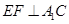 ;(Ⅱ)求三棱锥
;(Ⅱ)求三棱锥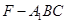 的体积。
的体积。(I)证明:见解析;
(Ⅱ)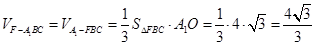
(Ⅱ)
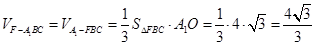
本题主要考查了直线与平面垂直的判定,以及棱柱、棱锥、棱台的体积,考查空间想象能力、运算能力和推理论证能力,属于基础题.
(1)欲证EF⊥A'C,可先证EF⊥平面A'EC,根据直线与平面垂直的判定定理可知只需证EF⊥平面A'EC内两相交直线垂直,而EF⊥A'E,EF⊥EC,EC∩A‘E=E,满足定理条件;
(2)先根据题意求出S△FBC,将求三棱锥F-A′BC的体积转化成求三棱锥A′-BCF的体积,再根据三棱锥的体积公式求解即可.
(I)证明:在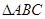 中,
中,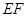 是等腰直角
是等腰直角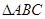 的中位线,EF//BC
的中位线,EF//BC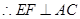 在四棱锥
在四棱锥 中,
中,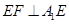 ,
,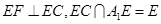 ,
, 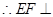 平面
平面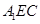 , 又
, 又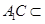 平面
平面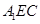 ,
, 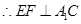
(Ⅱ)解:在直角梯形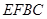 中,
中,
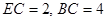 ,
,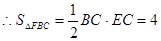
又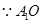 垂直平分
垂直平分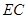 ,
,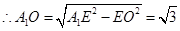
 三棱锥
三棱锥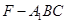 的体积为:
的体积为:
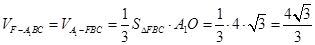
(1)欲证EF⊥A'C,可先证EF⊥平面A'EC,根据直线与平面垂直的判定定理可知只需证EF⊥平面A'EC内两相交直线垂直,而EF⊥A'E,EF⊥EC,EC∩A‘E=E,满足定理条件;
(2)先根据题意求出S△FBC,将求三棱锥F-A′BC的体积转化成求三棱锥A′-BCF的体积,再根据三棱锥的体积公式求解即可.
(I)证明:在
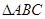 中,
中,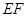 是等腰直角
是等腰直角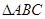 的中位线,EF//BC
的中位线,EF//BC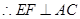 在四棱锥
在四棱锥 中,
中,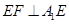 ,
,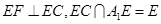 ,
, 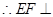 平面
平面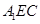 , 又
, 又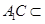 平面
平面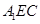 ,
, 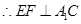
(Ⅱ)解:在直角梯形
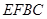 中,
中,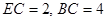 ,
,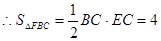
又
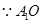 垂直平分
垂直平分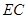 ,
,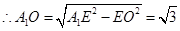
 三棱锥
三棱锥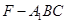 的体积为:
的体积为: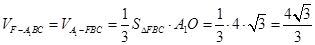

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
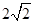 ,且
,且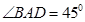 ,以BD为折线,把
,以BD为折线,把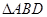 折起,使平面
折起,使平面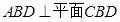 ,连AC.
,连AC.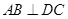 (Ⅱ)求二面角B-AC-D平面角的大小;
(Ⅱ)求二面角B-AC-D平面角的大小;

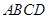 中,
中,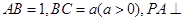 平面
平面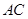 ,且
,且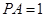 ,若在
,若在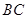 边上存在一点
边上存在一点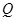 ,使得
,使得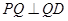 ,则
,则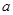 的取值范围是
的取值范围是 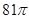
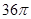
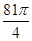
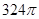

 、
、 、
、 ,则这个长方体的外接球的表面积为 .
,则这个长方体的外接球的表面积为 .