题目内容
在极坐标系内,已知曲线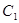 的方程为
的方程为 ,以极点为原点,极轴方向为
,以极点为原点,极轴方向为 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线
正半轴方向,利用相同单位长度建立平面直角坐标系,曲线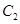 的参数方程为
的参数方程为 (
(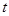 为参数).
为参数).
(1) 求曲线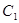 的直角坐标方程以及曲线
的直角坐标方程以及曲线 的普通方程;
的普通方程;
(2) 设点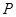 为曲线
为曲线 上的动点,过点
上的动点,过点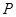 作曲线
作曲线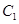 的两条切线,求这两条切线所成角余弦值的取值范围.
的两条切线,求这两条切线所成角余弦值的取值范围.
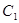 的方程为
的方程为 ,以极点为原点,极轴方向为
,以极点为原点,极轴方向为 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线
正半轴方向,利用相同单位长度建立平面直角坐标系,曲线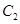 的参数方程为
的参数方程为 (
(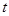 为参数).
为参数).(1) 求曲线
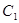 的直角坐标方程以及曲线
的直角坐标方程以及曲线 的普通方程;
的普通方程;(2) 设点
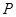 为曲线
为曲线 上的动点,过点
上的动点,过点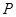 作曲线
作曲线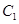 的两条切线,求这两条切线所成角余弦值的取值范围.
的两条切线,求这两条切线所成角余弦值的取值范围. (1)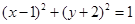 ,
,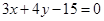 ;(2)
;(2) 
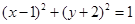 ,
,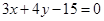 ;(2)
;(2) 
试题分析:本小题主要考查极坐标与参数方程的相关知识,具体涉及到极坐标方程与平面直角坐标方程的互化、直线与曲线的位置关系以及有关距离等知识内容.(1)利用极坐标转化公式直接转化求圆的方程,利用消掉参数的方法得到直线的普通方程;(2)首先确定两切线成角
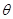 最大的情况,借助点到直线的距离和二倍角公式探求余弦值最小,进而得到取值范围.
最大的情况,借助点到直线的距离和二倍角公式探求余弦值最小,进而得到取值范围.试题解析:(1) 对于曲线
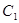 的方程为
的方程为 ,
,可化为直角坐标方程
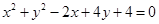 ,即
,即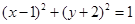 ;
;对于曲线
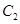 的参数方程为
的参数方程为 (
(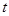 为参数),可化为普通方程
为参数),可化为普通方程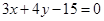 . (5分)
. (5分)(2) 过圆心
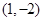 点作直线
点作直线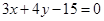 的垂线,此时两切线成角
的垂线,此时两切线成角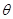 最大,即余弦值最小. 则由点到直线的距离公式可知,
最大,即余弦值最小. 则由点到直线的距离公式可知,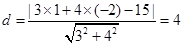 ,则
,则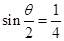 ,因此
,因此 ,
,因此两条切线所成角的余弦值的取值范围是
 . (10分)
. (10分) 
练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
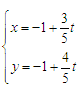 (为参数),曲线C的极坐标方程为
(为参数),曲线C的极坐标方程为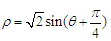 .
.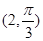 到圆
到圆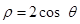 的圆心的距离为( ).
的圆心的距离为( ).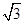 C.
C. 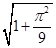 D
D 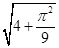
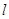 的方程为
的方程为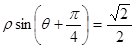 ,则点
,则点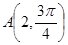 到直线
到直线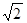
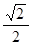
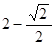
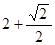
 和
和 ,则
,则 、
、 两点间的距离是 .
两点间的距离是 . 
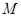 点的极坐标为
点的极坐标为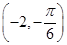 ,则
,则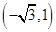
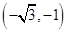
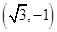
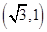
 的直线
的直线 与极轴的夹角
与极轴的夹角 ,若将
,若将 的形式,则
的形式,则

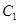 的参数方程为
的参数方程为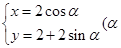 为参数),M为
为参数),M为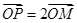 ,点P的轨迹为曲线
,点P的轨迹为曲线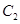 .已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线
.已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线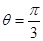 与
与