题目内容
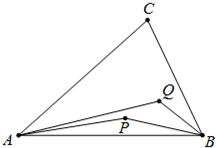 如图,设P,Q为△ABC内的两点,且
如图,设P,Q为△ABC内的两点,且| AP |
| 2 |
| 3 |
| AB |
| 1 |
| 4 |
| AC |
| AQ |
| 3 |
| 5 |
| AB |
| 1 |
| 3 |
| AC |
| 3 |
| 4 |
| 3 |
| 4 |
分析:如图所示,分别过点P,Q作PD⊥AB,QE⊥AB,垂足分别为D,E.在△APD中,
=
-
,利用向量垂直与数量积的关系可得
•
=0,
把已知代入得到|
|=
|
|+
|
|cosA.利用勾股定理可得|
|2=
2-|
|2,于是|
|=
|
|sinA.同理可得|
|=
|
|sinA.
由此可得
=
.
| PD |
| AD |
| AP |
| PD |
| AB |
把已知代入得到|
| AD |
| 2 |
| 3 |
| AB |
| 1 |
| 4 |
| AC |
| PD |
| AP |
| AD |
| PD |
| 1 |
| 4 |
| AC |
| QE |
| 1 |
| 3 |
| AC |
由此可得
| S△APB |
| S△AQB |
|
| ||
|
|
解答:解:如图所示,分别过点P,Q作PD⊥AB,QE⊥AB,垂足分别为D,E.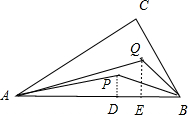
在△APD中,
=
-
,
∵
⊥
,∴
•
=0,
∴(
-
)•
=
•
-
•
=0,
∴
•
=
•
=(
+
)•
=
2+
•
,
∴|
|•|
|=
|
|2+
|
| |
|cosA,
得到|
|=
|
|+
|
|cosA.
∴|
|2=
2-|
|2=(
+
)2-(
|
|+
|
|cosA)2
=
2-
|
|2cos2A=
|
|2sin2A,
∴|
|=
|
|sinA.
同理可得|
|=
|
|sinA.
∴
=
=
=
.
故答案为
.

在△APD中,
| PD |
| AD |
| AP |
∵
| PD |
| AB |
| PD |
| AB |
∴(
| AD |
| AP |
| AB |
| AD |
| AB |
| AP |
| AB |
∴
| AD |
| AB |
| AP |
| AB |
| 2 |
| 3 |
| AB |
| 1 |
| 4 |
| AC |
| AB |
| 2 |
| 3 |
| AB |
| 1 |
| 4 |
| AC |
| AB |
∴|
| AD |
| AB |
| 2 |
| 3 |
| AB |
| 1 |
| 4 |
| AC |
| AB |
得到|
| AD |
| 2 |
| 3 |
| AB |
| 1 |
| 4 |
| AC |
∴|
| PD |
| AP |
| AD |
| 2 |
| 3 |
| AB |
| 1 |
| 4 |
| AC |
| 2 |
| 3 |
| AB |
| 1 |
| 4 |
| AC |
=
| 1 |
| 16 |
| AC |
| 1 |
| 16 |
| AC |
| 1 |
| 16 |
| AC |
∴|
| PD |
| 1 |
| 4 |
| AC |
同理可得|
| QE |
| 1 |
| 3 |
| AC |
∴
| S△APB |
| S△AQB |
|
| ||
|
|
| ||||
|
| 3 |
| 4 |
故答案为
| 3 |
| 4 |
点评:熟练掌握向量垂直与数量积的关系、勾股定理和三角形的面积计算公式等是解题的关键.

练习册系列答案
相关题目
 如图,设P、Q为△ABC内的两点,且
如图,设P、Q为△ABC内的两点,且| AP |
| 2 |
| 5 |
| AB |
| 1 |
| 5 |
| AC |
| AQ |
| 2 |
| 3 |
| AB |
| 1 |
| 4 |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,设P,Q为△ABC内的两点,且
如图,设P,Q为△ABC内的两点,且


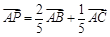 ,
, ,则△ABP的面积与△ABQ的面积之比为( )
,则△ABP的面积与△ABQ的面积之比为( ) B.
B.
 D.
D.
