题目内容
如图，设P，Q为△ABC内的两点，且| AP |
| 1 |
| 4 |
| AB |
| 1 |
| 3 |
| AC |
| AQ |
| 1 |
| 5 |
| AB |
| 3 |
| 4 |
| AC |
分析：利用向量的运算法则：平行四边形法则作出P，利用同底的三角形的面积等于高的比求出
，同理求出
，两个式子比求出△ABP的面积与△ABQ的面积之比．
| △ABP的面积 |
| △ABC的面积 |
| △ABQ的面积 |
| △ABC的面积 |
解答：解：设
=
，
=
则
=
+
由平行四边形法则知NP∥AB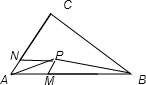
所以
=
=
同理
=
故
=
故选C．
| AM |
| 1 |
| 4 |
| AB |
| AN |
| 1 |
| 3 |
| AC |
则
| AP |
| AM |
| AN |
由平行四边形法则知NP∥AB
所以
| △ABP的面积 |
| △ABC的面积 |
|
| ||
|
|
| 1 |
| 3 |
同理
| △ABQ的面积 |
| △ABC的面积 |
| 3 |
| 4 |
故
| △ABP的面积 |
| △ABQ的面积 |
| 4 |
| 9 |
故选C．
点评：本题以向量为载体，考查向量的运算法则：平行四边形法则以及三角形的面积公式．属于基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
如图，设P、Q为△ABC内的两点，且| AP |
| 2 |
| 5 |
| AB |
| 1 |
| 5 |
| AC |
| AQ |
| 2 |
| 3 |
| AB |
| 1 |
| 4 |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
， 
＝
＋
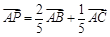，则△ABP的面积与△ABQ的面积之比为( )
B． 
C． 
， 
＝
＋
，则△ABP的面积与△ABQ的面积之比为( )
B． 
C． 
，
，则△ABP的面积与△ABQ的面积之比为（ ）
B．
D．
