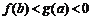题目内容
如图,在 轴的正半轴上依次有点
轴的正半轴上依次有点 ,其中点
,其中点 、
、 ,且
,且
 ,在射线
,在射线 上依次有点
上依次有点 ,点
,点 的坐标为
的坐标为 ,且
,且

 .
.
(1)求点 、
、 的坐标;
的坐标;
(2)设四边形 面积为
面积为 ,解答下列问题:
,解答下列问题:
① 问 中是否存在连续的三项
中是否存在连续的三项 ,
, ,
,
( )恰好成等差数列?若存在,求出所
)恰好成等差数列?若存在,求出所
有这样的三项;若不存在,请说明理由;
② 求满足不等式 的所有自然数
的所有自然数 .
.
(1) ,
,



 的坐标
的坐标 ,
,
 (
( )且
)且
 是以
是以 为首项,
为首项, 为公差的等差数列
为公差的等差数列

 的坐标为
的坐标为 .
.
(2)连接 ,设四边形
,设四边形 的面积为
的面积为 ,
,
则

 .-
.-
① 设连续的三项 ,
, ,
, (
( )成等差数列,
)成等差数列,
则有, ,
,
即 ,
,
解得 .
.
所以,存在连续的三项 ,
, ,
, 恰好成等差数列.
恰好成等差数列.
② 
 数列
数列 是单调递减数列.
是单调递减数列.
由于

用计算器可知 ,
, .
.
由于数列 是单调递减数列,
是单调递减数列,
所以,满足不等式 的所有自然数
的所有自然数 为不小于9的所有自然数.
为不小于9的所有自然数.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
从某项有400人参加的群众性运动的达标测试中,随机地抽取50人的成绩统计成如下 表,则400人的成绩的标准差的点估计值是 .
表,则400人的成绩的标准差的点估计值是 .
| 分数 | 5 | 4 | 3 | 2 | 1 |
| 人数 | 5 | 15 | 20 | 5 | 5 |

 ,且
,且 ,则
,则 的值用
的值用 表示为 .
表示为 . 的一个法向量
的一个法向量 ,其中
,其中 ,则
,则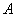 ,
,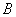 为两个不同的定点,动点
为两个不同的定点,动点 满足:
满足: (
( 为实常数),则动点
为实常数),则动点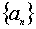 是公差为2的等差数列,若
是公差为2的等差数列,若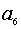 是
是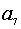 和
和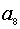 的等比中项,则
的等比中项,则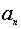 =________.
=________.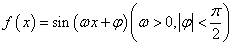 的最小正周期是
的最小正周期是 ,若其图象向右平移
,若其图象向右平移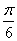 个单位后得到的函数为奇函数,则函数
个单位后得到的函数为奇函数,则函数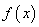 的图象
的图象 对称 B.关于直线
对称 B.关于直线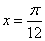 对称
对称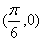 对称 D.关于直线
对称 D.关于直线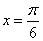 对称
对称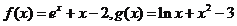 . 若实数a, b满足
. 若实数a, b满足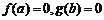 , 则
, 则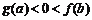 B.
B.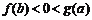
 D.
D.