题目内容
10．已知集合 A={x|x＞0}，B={-1，0，1}，则 A∩B={1}．分析 利用交集的性质求解．
解答 解：∵集合A={x|x＞0}，B={-1，0，1}，
∴A∩B={1}．
故答案为：{1}．
点评 本题考查交集的求法，是基础题，解题时要注意交集性质的合理运用．
练习册系列答案
相关题目
1．点A位于双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）上，F1F2是它的两个焦点，求△AF1F2的重心G的轨迹方程．
5．
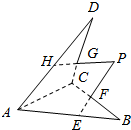已知E、F、G、H依次为空间四边形ABCD的边AB、BC、CD、DA上的点，且直线EF交直线HG于点P，则点P的位置是必处在（ ）的上面．
已知E、F、G、H依次为空间四边形ABCD的边AB、BC、CD、DA上的点，且直线EF交直线HG于点P，则点P的位置是必处在（ ）的上面．| A． | BD | B． | AD | C． | AC | D． | 平面BCD之内 |
15．观察下列的图形中小正方形的个数，则第6个图中有（ ）个小正方形，第n个图中有（ ）个小正方形（ ）
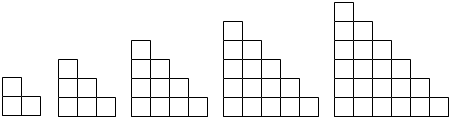
| A． | 28，$\frac{（n+1）（n+2）}{2}$ | B． | 14，$\frac{（n+1）（n+2）}{2}$ | C． | 28，$\frac{n}{2}$ | D． | 12，$\frac{{n}^{2}+n}{2}$ |
2．若复数Z=$\frac{a+3i}{1-2i}$（a∈R，i是虚数单位）是纯虚数，则在复平面内Z对应点的坐标为（ ）
| A． | （0，2） | B． | （0，3i ） | C． | （0，3） | D． | （0，2i） |
19．函数y=${log_{\frac{1}{2}}}$（3x-x2-2）的单调递减区间是（ ）
| A． | （1，2） | B． | （2，+∞） | C． | （1，$\frac{3}{2}$） | D． | （$\frac{3}{2}$，+∞） |