题目内容
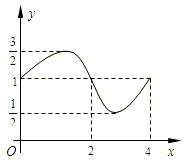 函数f(x)=Asin(ωx+?)+b的图象如下,则S=f(0)+f(1)+…+f(2011)=________.
函数f(x)=Asin(ωx+?)+b的图象如下,则S=f(0)+f(1)+…+f(2011)=________.
2012
分析:由图象如图求得 A= ,周期为4,由f(0)+f(1)+f(2)+f(3)=4可得要求的式子等于 503×[f(0)+f(1)+f(2)+f(3)],从而得出结果.
,周期为4,由f(0)+f(1)+f(2)+f(3)=4可得要求的式子等于 503×[f(0)+f(1)+f(2)+f(3)],从而得出结果.
解答:由函数f(x)=Asin(ωx+?)(ω>0,A>0,0<?<π)的部分图象如图所示,可得 A=2,
函数的周期为4.
又∵f(0)=1,f(1)= ,f(2)=1,f(3)=
,f(2)=1,f(3)= ,
,
∴f(0)+f(1)+f(2)+f(3)=1+ +1+
+1+ =4.
=4.
则f(4k)+f(4k+1)+f(4k+2)+f(4k+3)=4,k∈Z
∴f(0)+f(1)+f(2)+f(3)+…+f(2011)
=503×[f(0)+f(1)+f(2)+f(3)]=503×4=2012.
故答案为2012
点评:本题主要考查利用函数y=Asin(ωx+∅)的部分图象求函数的解析式,函数y=Asin(ωx+∅)的周期性的应用,属于中档题.
分析:由图象如图求得 A=
 ,周期为4,由f(0)+f(1)+f(2)+f(3)=4可得要求的式子等于 503×[f(0)+f(1)+f(2)+f(3)],从而得出结果.
,周期为4,由f(0)+f(1)+f(2)+f(3)=4可得要求的式子等于 503×[f(0)+f(1)+f(2)+f(3)],从而得出结果.解答:由函数f(x)=Asin(ωx+?)(ω>0,A>0,0<?<π)的部分图象如图所示,可得 A=2,
函数的周期为4.
又∵f(0)=1,f(1)=
 ,f(2)=1,f(3)=
,f(2)=1,f(3)= ,
,∴f(0)+f(1)+f(2)+f(3)=1+
 +1+
+1+ =4.
=4.则f(4k)+f(4k+1)+f(4k+2)+f(4k+3)=4,k∈Z
∴f(0)+f(1)+f(2)+f(3)+…+f(2011)
=503×[f(0)+f(1)+f(2)+f(3)]=503×4=2012.
故答案为2012
点评:本题主要考查利用函数y=Asin(ωx+∅)的部分图象求函数的解析式,函数y=Asin(ωx+∅)的周期性的应用,属于中档题.

练习册系列答案
相关题目
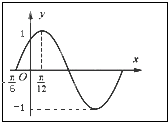 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
 如图所示的是定义域为R的函数f(x)=Asin(ωx+φ)(其中ω>0,φ∈[-π,π))的部分图象,则不等式
如图所示的是定义域为R的函数f(x)=Asin(ωx+φ)(其中ω>0,φ∈[-π,π))的部分图象,则不等式