题目内容
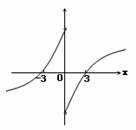
如图所示的是定义域为R的函数f（x）=Asin（ωx+φ）（其中ω＞0，φ∈[-π，π））的部分图象，则不等式f(x)＞| 3 |
分析：依题意，可求得A=2，由由函数的图象经过的特殊点，列出方程求出ω，φ．得到函数的解析式然后求出不等式的解集．
解答：解：由图知，A=2；
f（x）=2sin（ωx+φ）经过（0，
），（
，-2），且在该处是第一个蒸饭箱的最小值点，
∴2sinφ=
，2sin（ω×
+φ）=-2，
∴φ=
，ω×
+
=
，
∴ω=2．
∴f（x）的解析式为：f（x）=2sin（2x+
）．
∵f(x)＞
，
∴2sin（2x+
）＞
．
+2kπ＜2x+
＜2kπ+
，k∈Z．
解得kπ＜x＜kπ+
，k∈Z．
不等式f(x)＞
的解集为：{x|kπ＜x＜kπ+
，k∈Z}．
故答案为：{x|kπ＜x＜kπ+
，k∈Z}．
f（x）=2sin（ωx+φ）经过（0，
| 3 |
| 7π |
| 12 |
∴2sinφ=
| 3 |
| 7π |
| 12 |
∴φ=
| π |
| 3 |
| 7π |
| 12 |
| π |
| 3 |
| 3π |
| 2 |
∴ω=2．
∴f（x）的解析式为：f（x）=2sin（2x+
| π |
| 3 |
∵f(x)＞
| 3 |
∴2sin（2x+
| π |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
解得kπ＜x＜kπ+
| π |
| 6 |
不等式f(x)＞
| 3 |
| π |
| 6 |
故答案为：{x|kπ＜x＜kπ+
| π |
| 6 |
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，确定φ的值是难点，考查观察与运算能力，注意三角不等式的解法，属于中档题．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
＜x≤1
或0＜x≤1
或0＜x≤1}
＜x≤1}
＜x≤1}
或0＜x≤1}
