题目内容
正三角形ABC的边长为2，则| AB |
| BC |
分析：要求数量积，需要知道模和夹角，条件中的模给出，而由题目所给的条件可知夹角不是三角形的内角，而是内角的补角，这是易错点，向量的夹角是把向量的起点放在一起所形成的角．
解答：解：由题意知：两个向量的夹角是120°，
∴
•
=2×2×cos120°
=-2，
故答案为：-2．
∴
| AB |
| BC |
=-2，
故答案为：-2．
点评：本题是向量数量积的运算，条件中给出两个向量的模和两向量的夹角，代入数量积的公式运算即可，只是题目所给的夹角容易出错，易错为三角形的内角．
练习册系列答案
相关题目
已知正三角形ABC的边长为a，那么三角形ABC根据斜二测画法得到的平面直观图三角形A′B′C′的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
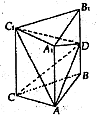（2011•烟台一模）如图：在三棱柱ABC-A1B1C1中，底面正三角形ABC的边长为3，D为侧棱BB1的中点，且DB=2，∠ABD=90°，DA=DC．