题目内容
正三角形ABC的边长为1,设
=
,
=
,
=
,那么
•
+
•
+
•
的值是( )
. |
| AB |
. |
| c |
. |
| BC |
. |
| a |
. |
| CA |
. |
| b |
| a |
| b |
| b |
| c |
| c |
| a |
分析:由题意可知向量
,
,
的模均为1,且三个向量的夹角均为120°,然后直接代入向量的数量积公式计算.
| a |
| b |
| c |
解答:解:由题意可知,|
|=|
|=|
|=1,且<
,
>=<
,
>=<
,
>=120°.
所以
•
+
•
+
•
=|
||
|cos120°+|
||
|cos120°+|
||
|cos120°
=1•1•cos120°+1•1•cos120°+1•1•cos120°
=3cos120°=-
.
故选C.
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
所以
| a |
| b |
| b |
| c |
| c |
| a |
| a |
| b |
| b |
| c |
| c |
| a |
=1•1•cos120°+1•1•cos120°+1•1•cos120°
=3cos120°=-
| 3 |
| 2 |
故选C.
点评:本题考查了平面向量的数量积运算,解答的关键是熟记公式及注意向量的夹角,是基础题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
已知正三角形ABC的边长为a,那么三角形ABC根据斜二测画法得到的平面直观图三角形A′B′C′的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
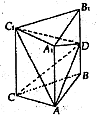 (2011•烟台一模)如图:在三棱柱ABC-A1B1C1中,底面正三角形ABC的边长为3,D为侧棱BB1的中点,且DB=2,∠ABD=90°,DA=DC.
(2011•烟台一模)如图:在三棱柱ABC-A1B1C1中,底面正三角形ABC的边长为3,D为侧棱BB1的中点,且DB=2,∠ABD=90°,DA=DC.