题目内容
已知函数 。
。
(Ⅰ)若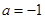 ,求函数
,求函数 的单调区间并比较
的单调区间并比较 与
与 的大小关系
的大小关系
(Ⅱ)若函数 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为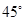 ,对于任意的
,对于任意的 ,函数
,函数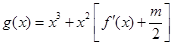 在区间
在区间 上总不是单调函数,求
上总不是单调函数,求 的取值范围;
的取值范围;
(Ⅲ)求证: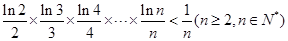 。
。
 。
。(Ⅰ)若
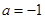 ,求函数
,求函数 的单调区间并比较
的单调区间并比较 与
与 的大小关系
的大小关系(Ⅱ)若函数
 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为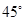 ,对于任意的
,对于任意的 ,函数
,函数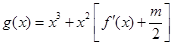 在区间
在区间 上总不是单调函数,求
上总不是单调函数,求 的取值范围;
的取值范围;(Ⅲ)求证:
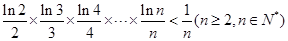 。
。(I) 的单调增区间为
的单调增区间为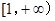 ;减区间为
;减区间为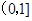 ,
,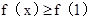 .
.
(II)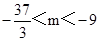 .
.
(III)证明见解析.
 的单调增区间为
的单调增区间为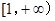 ;减区间为
;减区间为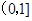 ,
,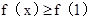 .
.(II)
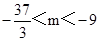 .
.(III)证明见解析.
试题分析:(I)通过求导数,解
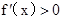 得增区间;解
得增区间;解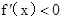 得减区间.
得减区间.驻点处得到最小值,比较得到
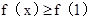 .
.(II)通过确定
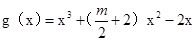 ,
,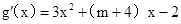 .
.根据
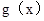 在区间
在区间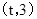 上总不是单调函数,且
上总不是单调函数,且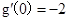 ,
,得到
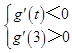 ,转化成“对于任意的
,转化成“对于任意的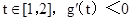 恒成立”
恒成立”依据
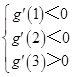 ,求得
,求得 的范围.
的范围.解答本题的关键是将问题加以转化,应用导数知识予以处理.
(III)利用
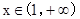 时,
时,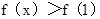 ,得到
,得到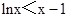 对一切
对一切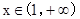 成立.
成立.从而应用
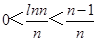 对乘积式中的各个因子进行“放缩”,达到证明目的.
对乘积式中的各个因子进行“放缩”,达到证明目的.∴
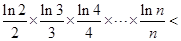
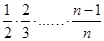 =
=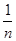 .
.试题解析:(I)当
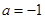 时
时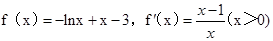 .
.令
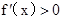 ,解得
,解得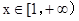 ;令
;令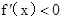 ,解得
,解得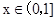 ,
,所以,
 的单调增区间为
的单调增区间为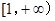 ;减区间为
;减区间为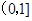
所以
 ,所以
,所以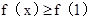 .
.(II)∵
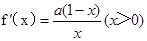
∴
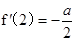 ,得
,得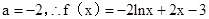
∴
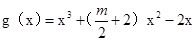 ,
,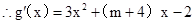 .
.∵
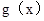 在区间
在区间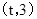 上总不是单调函数,且
上总不是单调函数,且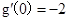 ,
,∴
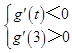
由题意知:对于任意的
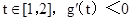 恒成立,
恒成立,所以有
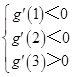 ,∴
,∴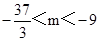
(III)证明如下:由(1)可知
当
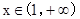 时,
时,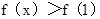 ,即
,即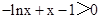 ,
,∴
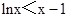 对一切
对一切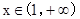 成立,
成立,∵
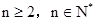 ,则有
,则有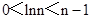 ,∴
,∴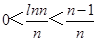 ,
,∴
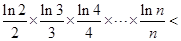
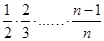 =
=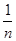 .
.故
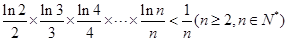 .
.
练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
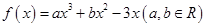 在点
在点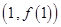 处的切线方程为
处的切线方程为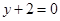 .
.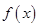 的解析式;
的解析式;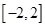 上任意两个自变量的值
上任意两个自变量的值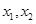 都有
都有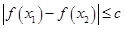 ,求实数
,求实数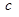 的最小值;
的最小值;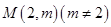 可作曲线
可作曲线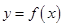 的三条切线,求实数
的三条切线,求实数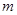 的取值范围.
的取值范围.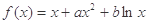 ,曲线
,曲线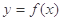 过点P(1,0),且在P点处的切斜线率为2.
过点P(1,0),且在P点处的切斜线率为2.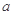 ,
,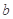 的值;
的值;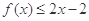 .
.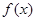
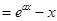 ,其中
,其中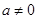 .
.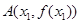 ,
,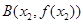
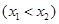 ,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使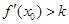 成立?若存在,求
成立?若存在,求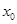 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. ,
, .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间 上是减函数,求
上是减函数,求 的取值范围.
的取值范围. 在
在 处的切线方程为
处的切线方程为 ,则
,则 ______,
______, ______.
______. 在点
在点 处的切线与
处的切线与 轴的交点横坐标为
轴的交点横坐标为 ,则
,则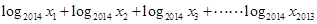 的值为( )
的值为( )



 ,则
,则 ( )
( )


