题目内容
已知函数 ,
, .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若 在区间
在区间 上是减函数,求
上是减函数,求 的取值范围.
的取值范围.
 ,
, .
.(Ⅰ)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(Ⅱ)若
 在区间
在区间 上是减函数,求
上是减函数,求 的取值范围.
的取值范围.(Ⅰ)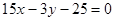 ;(Ⅱ)
;(Ⅱ)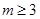 或
或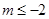 .
.
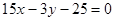 ;(Ⅱ)
;(Ⅱ)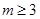 或
或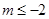 .
.试题分析:(Ⅰ)当
 时,
时,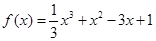 ,由导数的几何意义,先求
,由导数的几何意义,先求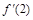 ,再利用点斜式求切线方程;(Ⅱ)先求得
,再利用点斜式求切线方程;(Ⅱ)先求得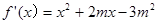 .令
.令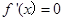 ,得
,得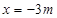 或
或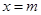 .再分
.再分 讨论,列不等式组求
讨论,列不等式组求 的范围.
的范围.试题解析:(Ⅰ)当
 时,
时,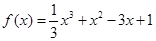 , 1分
, 1分又
 ,所以
,所以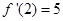 . 2分
. 2分又
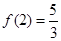 ,所以所求切线方程为
,所以所求切线方程为 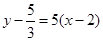 ,即
,即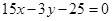 .所以曲线
.所以曲线 在点
在点 处的切线方程为
处的切线方程为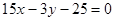 . 5分
. 5分(Ⅱ)方法一:因为
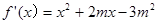 ,令
,令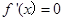 ,得
,得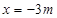 或
或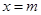 . 6分
. 6分当
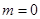 时,
时,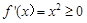 恒成立,不符合题意. 7分
恒成立,不符合题意. 7分当
 时,
时, 的单调递减区间是
的单调递减区间是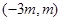 ,若
,若 在区间
在区间 上是减函数,
上是减函数,则
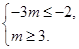 解得
解得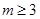 . 9分
. 9分当
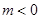 时,
时, 的单调递减区间是
的单调递减区间是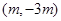 ,若
,若 在区间
在区间 上是减函数,则
上是减函数,则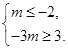 ,解得
,解得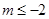 . 11分
. 11分综上所述,实数
 的取值范围是
的取值范围是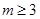 或
或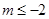 . 12分
. 12分(Ⅱ)方法二:
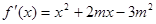 . 6分
. 6分因为
 在区间
在区间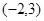 上是减函数,所以
上是减函数,所以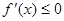 在
在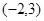 恒成立. 7分
恒成立. 7分因此
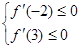 9分
9分则
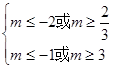 11分
11分故实数
 的取值范围
的取值范围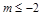 或
或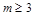 . 12分
. 12分
练习册系列答案
相关题目
 。
。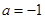 ,求函数
,求函数 的单调区间并比较
的单调区间并比较 的大小关系
的大小关系 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为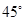 ,对于任意的
,对于任意的 ,函数
,函数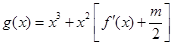 在区间
在区间 上总不是单调函数,求
上总不是单调函数,求 的取值范围;
的取值范围;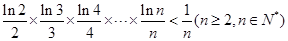 。
。 为圆心,
为圆心, (
( 区域(阴影部分)用于种植学校观赏植物,
区域(阴影部分)用于种植学校观赏植物, 区域用于种植花卉出售,其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元.
区域用于种植花卉出售,其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元,种植花卉的利润是每平方米80元,种植草皮的利润是每平方米30元.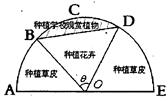
 (单位:弧度),用
(单位:弧度),用 表示弓形
表示弓形 ;
;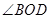 的大小才能使总利润最大?并求出该最大值.
的大小才能使总利润最大?并求出该最大值. ,
, 表示扇形的弧长)
表示扇形的弧长)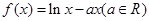
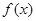 的单调区间;
的单调区间; 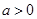 时,求函数
时,求函数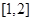 上的最小值.
上的最小值. ,
, ,
, .
.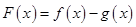 在
在 上单调递增;
上单调递增; 有四个零点,求
有四个零点,求 的取值范围.
的取值范围.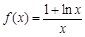 .
.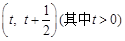 上存在极值,求实数
上存在极值,求实数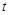 的取值范围;
的取值范围;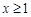 时,不等式
时,不等式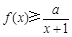 恒成立,求实数
恒成立,求实数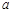 的取值范围.
的取值范围. 与曲线
与曲线 相切于点
相切于点 ,则
,则 。
。 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,当
,当 时,有
时,有 恒成立,则不等式
恒成立,则不等式 的解集是( )
的解集是( ) 在点
在点 处的切线与
处的切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,令
,令 ,则
,则 的值为___________.
的值为___________.