Question

7．函数f（x）（-2≤x≤2）的图象如图所示，则函数的最大值、最小值分别为（　　）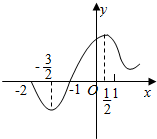

• A． f（2），f（-2）
• B． f（$\frac{1}{2}$），f（-1）
• C． f（$\frac{1}{2}$），f（-$\frac{3}{2}$）
• D． f（$\frac{1}{2}$），f（0）

Answer 1

分析 由图象得到函数的单调性，通过比较极值点与端点值的大小得答案．

解答 解：由图可知，f（x）在（-2，$-\frac{3}{2}$），（$\frac{1}{2}，1$）上为减函数，
在（$-\frac{3}{2}，\frac{1}{2}$），（1，2）上为增函数，且f（$-\frac{3}{2}$）＜f（-2）＜f（1）＜f（2）$＜f（\frac{1}{2}）$，
∴在[-2，2]上，函数的最大值、最小值分别为f（$\frac{1}{2}$），f（-$\frac{3}{2}$）．
故选：C．

点评 本题考查函数的图象，考查了学生学生的读图能力，是基础题．