题目内容
18.某几何体的三视图如图所示,则该几何体的体积为3$\sqrt{3}$.
分析 由三视图可知该几何体为直三棱柱,底面是边长为2的正三角形,高为3,带入体积公式即可求出体积.
解答 解:由三视图可知几何体为底面是边长为2的正三角形,高为3的直三棱柱,
∴V=$\frac{1}{2}$•2$•\sqrt{3}$•3=3$\sqrt{3}$.
故答案为3$\sqrt{3}$.
点评 本题考查了空间几何体的结构特征和三视图,以及体积计算,是基础题.

练习册系列答案
相关题目
9.下列各式因式分解正确的是( )
| A. | $\frac{1}{2}$a2+a+$\frac{1}{2}$=a2+2a+1=(a+1)2 | B. | a2+ab-6b2=a(a+b)-6b2 | ||
| C. | a2-b2-a-b=(a+b)(a-b)-a-b | D. | a-2a2+a3=a(1-2a+a2)=a(1-a)2 |
6.当x∈[0,2π]时,使得不等式cosx≥$\frac{\sqrt{2}}{2}$成立的x的取值范围是( )
| A. | [$\frac{π}{4}$,2π] | B. | [0,$\frac{π}{4}$] | C. | [-$\frac{π}{4}$,$\frac{π}{4}$] | D. | [0,$\frac{π}{4}$]∪[$\frac{7π}{4}$,2π] |
3.若一等差数列前5项和为25,前10项和为100,则它的前15项的和为( )
| A. | 125 | B. | 200 | C. | 225 | D. | 275 |
7.函数f(x)(-2≤x≤2)的图象如图所示,则函数的最大值、最小值分别为( )
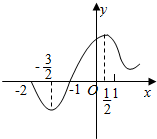

| A. | f(2),f(-2) | B. | f($\frac{1}{2}$),f(-1) | C. | f($\frac{1}{2}$),f(-$\frac{3}{2}$) | D. | f($\frac{1}{2}$),f(0) |