题目内容
17．计算：$\frac{{x}^{2}+x-6}{x-3}$÷$\frac{x+3}{{x}^{2}-x-6}$．分析 把二次三项式分解，然后利用有理指数幂的运算性质化简得答案．
解答 解：$\frac{{x}^{2}+x-6}{x-3}$÷$\frac{x+3}{{x}^{2}-x-6}$
=$\frac{（x-2）（x+3）}{x-3}×\frac{（x-3）（x+2）}{x+3}$
=（x-2）（x+2）=x2-4．
点评 本题考查有理指数幂的运算性质，考查了有理指数幂的化简求值，是基础题．
练习册系列答案
相关题目
7．函数f（x）（-2≤x≤2）的图象如图所示，则函数的最大值、最小值分别为（ ）
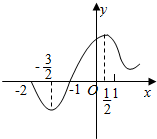
| A． | f（2），f（-2） | B． | f（$\frac{1}{2}$），f（-1） | C． | f（$\frac{1}{2}$），f（-$\frac{3}{2}$） | D． | f（$\frac{1}{2}$），f（0） |
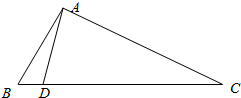如图，在△ABC中，已知点D在BC边上，AD•sin∠C+AC•sin∠ADC=DC•sin∠DAC，sin∠BAC=$\frac{2\sqrt{2}}{3}$，AB=3$\sqrt{2}$，AD=3．
如图为函数y=Asin（ωx+ϕ）+c（A＞0，ω＞0，ϕ＞0）图象的一部分，求此函数的解析式．