题目内容
2．已知a＞b，b为常数，则y=a+$\frac{1}{a-b}$的最小值为2+b．分析 利用基本不等式求解函数的最小值即可．
解答 解：a＞b，b为常数，a-b＞0，
则y=a+$\frac{1}{a-b}$=a-b+$\frac{1}{a-b}$+b≥$2\sqrt{（a-b）•\frac{1}{a-b}}+b$=2+b，函数的最小值为2+b．当且仅当a=b+1时取等号．
y=a+$\frac{1}{a-b}$的最小值为2+b．
故答案为：2+b．
点评 本题考查基本不等式的应用，函数的最小值的求法，考查计算能力．
练习册系列答案
相关题目
12．
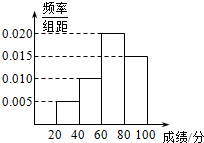学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次是[20，40），[40，60），[60，80），[80，100），若低于60分的人数是15人，则该班的学生人数和平均成绩分别是（ ）
学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次是[20，40），[40，60），[60，80），[80，100），若低于60分的人数是15人，则该班的学生人数和平均成绩分别是（ ）| A． | 45，67 | B． | 50，68 | C． | 55，69 | D． | 60，70 |
7．函数f（x）（-2≤x≤2）的图象如图所示，则函数的最大值、最小值分别为（ ）
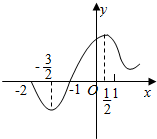
| A． | f（2），f（-2） | B． | f（$\frac{1}{2}$），f（-1） | C． | f（$\frac{1}{2}$），f（-$\frac{3}{2}$） | D． | f（$\frac{1}{2}$），f（0） |
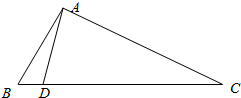如图，在△ABC中，已知点D在BC边上，AD•sin∠C+AC•sin∠ADC=DC•sin∠DAC，sin∠BAC=$\frac{2\sqrt{2}}{3}$，AB=3$\sqrt{2}$，AD=3．