Question

【题目】如图是一个几何体的平面展开图，其中四边形ABCD为正方形，△PDC, △PBC, △PAB, △PDA为全等的等边三角形，E、F分别为PA、PD的中点，在此几何体中，下列结论中错误的为 （ ）

A. 平面BCD⊥平面PAD B. 直线BE与直线AF是异面直线

C. 直线BE与直线CF共面 D. 面PAD与面PBC的交线与BC平行

Answer 1

【答案】A

【解析】

根据面面垂直的判断定理可判断不正确；根据异面直线的定义可判断正确；证明可判断正确；利用线面平行的性质可判断正确.

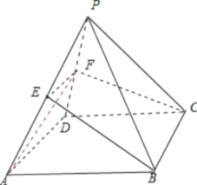
由展开图恢复原几何体如图所示：

折起后围成的几何体是正四棱锥，每个侧面都不与底面垂直，不正确；

由点不在平面内,直线不经过点,根据异面直线的定义可知：直线与直线异面，所以正确；

在中，由，

根据三角形的中位线定理可得,又，

故直线与直线共面，所以正确；

面，

由线面平行的性质可知面与面的交线与平行，正确，故选A.