题目内容
6.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{5},x∈[-1,1]}\\{x,x∈[1,π)}\\{sinx,x∈[π,3π]}\end{array}\right.$求f(x)在区间[-1,3π]上的定积分.分析 根据求分段函数求定积分,利用奇函数的性质,求得${∫}_{-1}^{3π}$f(x)dx的值.
解答 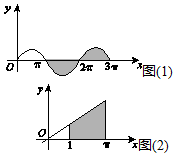 解:由定积分的几何意义知:
解:由定积分的几何意义知:
∵f(x)=x5是奇函数,故${∫}_{-1}^{1}$x5dx=0;
${∫}_{π}^{3π}$sinxdx=-cosx|${\;}_{π}^{3π}$=-(cos3π-cosπ)=0,(如图(1)所示);
${∫}_{1}^{π}$xdx=$\frac{1}{2}$x2|${\;}_{1}^{π}$=$\frac{1}{2}$(1+π)(π-1)=$\frac{1}{2}$(π2-1)(如图(2)所示).
∴${∫}_{-1}^{3π}$f(x)dx=${∫}_{-1}^{1}$x5dx+${∫}_{1}^{π}$xdx+${∫}_{π}^{3π}$sinxdx=0+$\frac{1}{2}$(π2-1)+0=$\frac{1}{2}$(π2-1).
点评 本题考查求分段函数的定积分及定积分的性质,属于基础题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
1.将某班的60名学生编号为01,02,…,60,采用系统抽样方法抽取一个容量为5的样本,且随机抽得的一个号码为04,则剩下的四个号码依次是( )
| A. | 09,14,19,24 | B. | 10,16,22,28 | C. | 16,28,40,52 | D. | 08,12,16,20 |
11.双曲线$\frac{{x}^{2}}{m}-\frac{{y}^{2}}{3+m}$=1的一个焦点为(2,0),则m的值为( )
| A. | $\frac{1}{2}$ | B. | 1或3 | C. | $\frac{1+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}-1}{2}$ |
15.定义运算:$a?b=\left\{\begin{array}{l}a,(a>b)\\ b,(a<b)\end{array}\right.$,例如2?3=3,则下列等式不能成立的是( )
| A. | (a?b)2=a2?b2 | B. | (a?b)?c=a?(b?c) | ||
| C. | (a?b)2=(b?a)2 | D. | c•(a?b)=(c•a)?(c•b)(c>0) |
16.设曲线y=xn+1(n∈N*)在点(1,1)处的切线与x轴的交点的横坐标为xn,则log2017x1+log2017x2+…+log2017x2016的值为( )
| A. | -log20172016 | B. | -1 | C. | log20172016-1 | D. | 1 |