题目内容
17．（$\frac{1}{\sqrt{x}}$-x2）10的展开式中x5的系数为210．分析 利用二项式展开式的通项公式，令x的指数等于5，求出r的值，再计算展开式中含x5项的系数．
解答 解：（$\frac{1}{\sqrt{x}}$-x2）10的展开式中，通项公式为：
Tr+1=${C}_{10}^{r}$•${（\frac{1}{\sqrt{x}}）}^{10-r}$•（-x2）r=（-1）r•${C}_{10}^{r}$•${x}^{\frac{5r}{2}-5}$，
令$\frac{5r}{2}$-5=5，解得r=4；
∴展开式中含x5项的系数为（-1）4•${C}_{10}^{4}$=210．
故答案为：210．
点评 本题考查了二项式展开式通项公式的应用问题，是基础题．
练习册系列答案
相关题目
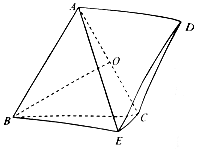在多面体ABCDE中，平面ABC⊥平面BCE，四边形ABED为平行四边形，AB=AC=BC=2，CE=1，BE=$\sqrt{5}$，O为AC的中点．
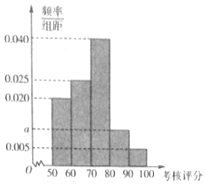2016年，某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》，为了解本省各家企业对环保的重视情况，从中抽取了40家企业进行考核评分，考核评分均在[50，100]内，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图如图（满分为100分）．
2．已知数列{an}满足an=$\left\{\begin{array}{l}{（\frac{1}{2}-a）n+1（n＜6）}\\{{a}^{n-5}（n≥6）}\end{array}\right.$若对于任意的n∈N*都有an＞an+1，则实数a的取值范围是（ ）
| A． | （0，$\frac{1}{2}$） | B． | （$\frac{1}{2}$，$\frac{7}{12}$） | C． | （$\frac{1}{2}$，1） | D． | （$\frac{7}{12}$，1） |