题目内容
数列{an}满足a1＝3，an－anan＋1＝1，An表示{an}的前n项之积，则A2 013＝________.
-1
解题思路：由a1＝3，an－anan＋1＝1，得an＋1＝
，所以a2＝
＝
，a3＝－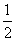
，a4＝3，所以{an}是以3为周期的数列，且a1a2a3＝－1，又2 013＝3×671，所以A2 013＝(－1)671＝－1.
练习册系列答案
相关题目
题目内容
数列{an}满足a1＝3，an－anan＋1＝1，An表示{an}的前n项之积，则A2 013＝________.
-1
解题思路：由a1＝3，an－anan＋1＝1，得an＋1＝，所以a2＝＝，a3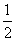＝－，a4＝3，所以{an}是以3为周期的数列，且a1a2a3＝－1，又2 013＝3×671，所以A2 013＝(－1)671＝－1.
B.
C.
D.
B．n3－5n2＋9n－4
是等比数列；
ω＞0)在(0,2]上恰有一个最大值1和一个最小值－1，则ω的取值范围为______．
AC，作直线AF与圆E相切于点F，连接EF交BC于点D，已知圆E的半径为2，∠EBC＝30°.
与
的夹角为120°，且|
＝λ
，则实数λ＝________．