题目内容

4．已知（1+ax）6=a0+a1x+a2x2+…+a6x6，若a2=${∫}_{0}^{3}$（x2+2）dx，则实数a的值为（　　）
A．1B．2C．±1D．±2

分析 根据定积分的计算和二项式展开式的通项公式分别求出a2，即可求出a的值．

解答 解：∵a2=${∫}_{0}^{3}$（x2+2）dx=（$\frac{1}{3}{x}^{3}+2x$）|${\;}_{0}^{3}$=9+6=15，且a2=C62a2=15a2，
∴15a2=15，
∴a=±1，
故选：C．

点评 本题主要考查定积分的计算和二项式定理的应用，二项式展开式的通项公式，求展开式中某项的系数，属于中档题

练习册系列答案
相关题目
14．设m，n是两条不同的直线，α，β是两个不同的平面，则下列命题中正确的是（　　）
A．若α∥β，m?α，n?β，则m∥nB．若α∥β，m∥α，n∥β，则m∥n
C．若m⊥α，n⊥β，m⊥n，则α∥βD．若m∥α，m?β，α∩β=n，则m∥n
15．已知z为虚数，且有|z|=$\sqrt{5}$，如果z2+2$\overline{z}$为实数．
（1）求：复数z；
（2）若z恰为实系数一元二次方程ax2+bx+c=0的根，试求出此方程．
12．求函数$y=\sqrt{x-5}+\sqrt{7-x}$的最大值．
19．若复数z满足（1+2i）•$\overline{z}$=|1-2i|2，其中$\overline{z}$是z的共轭复数，则z的虚部为（　　）
A．$\frac{-2\sqrt{5}}{5}$B．-2C．$\frac{2\sqrt{5}}{5}$D．2
9．若存在x∈（2，+∞）使不等式2x-m＜log2x成立，则实数m的取值范围为（3，+∞）．
16．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），A为椭圆E的右顶点，B，C分别为椭圆E的上、下顶点．
（I）若N为AC的中点，△BAN的面积为$\sqrt{2}$，椭圆的离心率为$\frac{\sqrt{2}}{2}$．求椭圆E的方程；
（Ⅱ）F为椭圆E的右焦点，线段CF的延长线与线段AB交于点M，与椭圆E交于点P，求$\frac{|CM|}{|CP|}$的最小值．
13．如图是一个程序框图，它的功能是（　　）
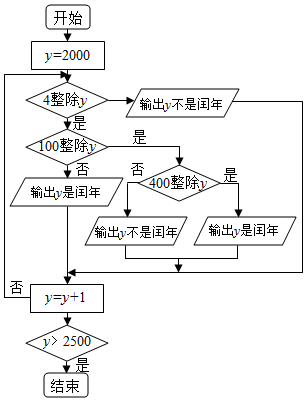
A．输出年份y∈[2000，2500）且y∈N“哪年是闰年”“哪年不是闰年”
B．输出年份y∈[2000，2500]且y∈N“哪年是闰年”“哪年不是闰年”
C．输出年份y∈[2000，2500）且y∈N“多少年是闰年”“多少年不是闰年”
D．输出年份y∈[2000，2500]且y∈N“多少年是闰年”“多少年不是闰年”
14．函数f（x）=x3-ax2-bx+a2在x=1处有极值10，则a+b=7．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网