题目内容
 如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
(1)求证:四边形EGGH是平行四边形.
(2)求证:EF∥平面ADC.
 证明:(1)连接 BD,因为HE是△ABD的中位线,所以,EH∥BD,且 EH=
证明:(1)连接 BD,因为HE是△ABD的中位线,所以,EH∥BD,且 EH= BD.
BD.同理,FG∥BD,且 FG=
 BD.因为 EH∥FG,且 EH=FG,
BD.因为 EH∥FG,且 EH=FG,所以,四边形 EFGH为平行四边形.
(2)∵由(1)知 EFGH为平行四边形,∴EF∥GH,而GH?平面ADC,
EF不在平面ADC 内,故有EF∥平面ADC.
分析:(1)利用三角形的中位线的性质可得 EH和 FG 平行且相等,即得EFGH为平行四边形.
(2)由EF∥GH,而GH?平面ADC,EF不在平面ADC 内可证的结论.
点评:本题考查证明线线平行、先面平行的方法,证明 EFGH为平行四边形是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
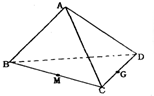 如图,空间四边形ABCD中,M、G分别是BC、CD的中点,则
如图,空间四边形ABCD中,M、G分别是BC、CD的中点,则| AB |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| BD |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,空间四边形ABCD的对棱AD、BC成60°的角,且AD=BC=4,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.
如图,空间四边形ABCD的对棱AD、BC成60°的角,且AD=BC=4,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H. 如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点. 如图,空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且
如图,空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且 如图,空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别在BC、CD上,且BG:GC=DH:HC=1:2
如图,空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别在BC、CD上,且BG:GC=DH:HC=1:2