题目内容
若实数a,b,c满足a2+b2+c2=1,则a2b2c2的最大值为 ;a+b+c的最小值为 ,3ab-3bc+2c2最大值为 .
考点:基本不等式
专题:转化思想,不等式
分析:①根据算术平均数不小于它们的几何平均数,利用a2+b2+c2≥3
,求出a2b2c2的最大值;
②根据a2+b2+c2≥
(a+b+c)2,求出a+b+c的最小值;
③讨论c=0以及c≠0时,利用判别式△≥0,求出3ab-3bc+2c2的最大值为.
| 3 | a2b2c2 |
②根据a2+b2+c2≥
| 1 |
| 3 |
③讨论c=0以及c≠0时,利用判别式△≥0,求出3ab-3bc+2c2的最大值为.
解答:
解:①∵a≥0,b≥0,c≥0时,
a+b+c≥3
,
∴a2+b2+c2≥3
,
∴a2b2c2≤(
)3=(
)3=
,当且仅当a=b=c=
时,“=”成立,
∴a2b2c2的最大值为
;
②∵a2+b2+c2≥
(a+b+c)2
∴(a+b+c)2≤3(a2+b2+c2)=3
∴-
≤a+b+c≤
∴a+b+c的最小值为-
;
③不妨考虑c,当c=0时,有3ab-3bc+2c2=3ab≤
=
,
当c≠0时,3ab-3bc+2c2=
=
,
设x=
,y=
,则可令M=3ab-3bc+2c2=
,
即有Mx2-3xy+My2+M+3y-2=0,
由于x为实数,则有判别式△1=9y2-4M(My2+M+3y-2)≥0,
即有(9-4M2)y2-12My-4M(M-2)≥0,
由于y为实数,则△2=144M2+16M(9-4M2)(M-2)≤0,
即有M(M-3)(2M2+2M-3)≤0,
由于求M的最大值,则M>0,则M≤3;
∴3ab-3bc+2c2最大值为3.
故答案为:
,-
,3.
a+b+c≥3
| 3 | abc |
∴a2+b2+c2≥3
| 3 | a2b2c2 |
∴a2b2c2≤(
| a2+b2+c2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 27 |
| ||
| 3 |
∴a2b2c2的最大值为
| 1 |
| 27 |
②∵a2+b2+c2≥
| 1 |
| 3 |
∴(a+b+c)2≤3(a2+b2+c2)=3
∴-
| 3 |
| 3 |
∴a+b+c的最小值为-
| 3 |
③不妨考虑c,当c=0时,有3ab-3bc+2c2=3ab≤
| 3(a2+b2)2 |
| 4 |
| 3 |
| 4 |
当c≠0时,3ab-3bc+2c2=
| 3ab-3bc+2c2 |
| a2+b2+c2 |
3•
| ||||||
(
|
设x=
| a |
| c |
| b |
| c |
| 3xy-3y+2 |
| x2+y2+1 |
即有Mx2-3xy+My2+M+3y-2=0,
由于x为实数,则有判别式△1=9y2-4M(My2+M+3y-2)≥0,
即有(9-4M2)y2-12My-4M(M-2)≥0,
由于y为实数,则△2=144M2+16M(9-4M2)(M-2)≤0,
即有M(M-3)(2M2+2M-3)≤0,
由于求M的最大值,则M>0,则M≤3;
∴3ab-3bc+2c2最大值为3.
故答案为:
| 1 |
| 27 |
| 3 |
点评:本题考查了不等式选修的应用问题,考查了灵活应用基本不等式的问题,是综合性题目.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
如图所示,AC1是正方体的一条体对角线,点P,Q分别为其在棱的中点,则PQ与AC1所成的角为( ) 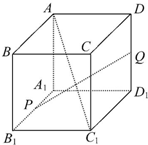

A、
| ||
B、
| ||
C、
| ||
D、
|
设变量x,y满足|x-1|+|y-a|≤1,若2x+y的最大值是5,则实数a的值是( )
| A、2 | B、1 | C、0 | D、-1 |
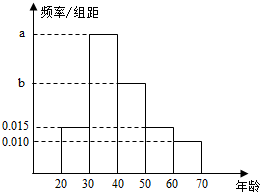 根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.
根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.
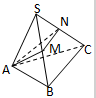 如图,△ABC外一点S,且SA⊥平面ABC,∠ABC=90°,AM⊥SB,AN⊥SC
如图,△ABC外一点S,且SA⊥平面ABC,∠ABC=90°,AM⊥SB,AN⊥SC