题目内容
当x∈（-2，1）时，f（x）=2x3+3x2-12x+1是（ ）
| A、单调递增函数 |
| B、单调递减函数 |
| C、部分单调增，部分单调减 |
| D、单调性不能确定 |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：先求出函数的导函数，然后在函数的定义域内解不等式fˊ（x）＞0的区间即可求出函数的单调增区间．
解答：
解：y′=f′（x）=6x2+6x-12
令f′（x）=6x2+6x-12＞0
解得：x∈（-∞，-2）和（1，+∞），
当x∈（-2，1）时，f′（x）=6x2+6x-12＜0．
函数在x∈（-2，1）是减函数．
故选：B．
令f′（x）=6x2+6x-12＞0
解得：x∈（-∞，-2）和（1，+∞），
当x∈（-2，1）时，f′（x）=6x2+6x-12＜0．
函数在x∈（-2，1）是减函数．
故选：B．
点评：本题主要考查了利用导数研究函数的单调性，单调性是函数的重要性质，属于中档题．
练习册系列答案
相关题目
| lim |
| △x→0 |
| f(x0+△x)-f(x0-△x) |
| 2△x |
A、
| ||
| B、f′（x0） | ||
| C、2f′（x0） | ||
| D、-f′（x0） |
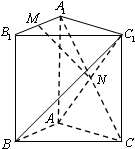三棱柱ABC-A1B1C1中，侧棱与底面垂直，∠ABC=90°，AB=BC=BB1，M是A1B1的中点，N是AC1与A1C的交点．