题目内容
18.已知AC、BD为圆O:x2+y2=4的两条相互垂直的弦,垂足为M(1,1),则四边形ABCD的面积的最大值为( )| A. | 6 | B. | 4$\sqrt{2}$ | C. | 5 | D. | 5$\sqrt{2}$ |
分析 设圆心到AC、BD的距离分别为d1、d2,则d12+d22 =2,代入面积公式S=$\frac{1}{2}$|AC||BD|,使用基本不等式求出四边形ABCD的面积的最大值.
解答  解:如图,连接OA、OD作OE⊥AC OF⊥BD垂足分别为E、F
解:如图,连接OA、OD作OE⊥AC OF⊥BD垂足分别为E、F
∵AC⊥BD
∴四边形OEMF为矩形
已知OA=OC=2,OM=$\sqrt{2}$,
设圆心O到AC、BD的距离分别为d1、d2,
则d12+d22=OM2=2.
四边形ABCD的面积为:S=$\frac{1}{2}$•|AC|(|BM|+|MD|),
从而:S=$\frac{1}{2}$|AC||BD|=2$\sqrt{(4-{{d}_{1}}^{2})(4-{{d}_{2}}^{2})}$≤8-(d12+d22)=6,
当且仅当d12 =d22时取等号,
故选:A.
点评 此题考查学生掌握垂径定理及勾股定理的应用,灵活运用两点间的距离公式化简求值,是一道中档题.解答关键是四边形面积可用互相垂直的2条对角线长度之积的一半来计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.如果命题P(n)对于n=k(k∈N*)时成立,那么它对n=k+2也成立.若P(n)对于n=2时成立,则下列结论正确的是( )
| A. | P(n)对所有正整数n成立 | B. | P(n)对所有正偶数n成立 | ||
| C. | P(n)对所有正奇数n成立 | D. | P(n)对所有大于1的正整数n成立 |
6.从数字1、2、3、4、5、6中随机取出3个不同的数字构成一个三位数,则这个三位数能被3整除的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
3.营养学家指出,成人良好的日常饮食应该至少提供75g的碳水化合物,60g的蛋白质,60g的脂肪,100g食物A含有12g的碳水化合物,8g的蛋白质,16g的脂肪,花费3元;而100g食物B含有12g的碳水化合物,16g的蛋白质,8g的脂肪,花费4元.
(Ⅰ)根据已知数据填写下表:
(Ⅱ)列车每天食用食物A和食物B所满足的不等式组;
(Ⅲ)为了满足营养学家指出的日常饮食要求,并且花费最低,每天需要食用食物A和食物B个多少g?
(Ⅰ)根据已知数据填写下表:
| 100g食物 | 碳水化合物/g | 蛋白质/g | 脂肪/g |
| A | |||
| B |
(Ⅲ)为了满足营养学家指出的日常饮食要求,并且花费最低,每天需要食用食物A和食物B个多少g?
10.{an}是首顶a1=1,公差d=3的等差数列,如果an=265,则序号n等于( )
| A. | 91 | B. | 90 | C. | 89 | D. | 88 |
8.(文)已知α∈R,sinα+2cosα=$\frac{\sqrt{10}}{2}$,则$\frac{(sinα+cosα+1)(sinα+cosα-1)}{(sinα-cosα)(sinα+cosα)}$=( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{3}{4}$ |
 如图,三棱锥P-ABC的三条侧棱两两垂直,即:PA⊥PB、PB⊥PC、PC⊥PA,且PO⊥平面ABC并交平面ABC于点O,请问点O是△ABC的什么心(内心、外心、垂心、重心、中心等)?并证明你的结论.
如图,三棱锥P-ABC的三条侧棱两两垂直,即:PA⊥PB、PB⊥PC、PC⊥PA,且PO⊥平面ABC并交平面ABC于点O,请问点O是△ABC的什么心(内心、外心、垂心、重心、中心等)?并证明你的结论.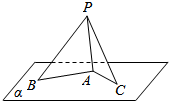 如图所示,8m高旗杆PA直立在地面α上,拉绳PB与地面α成30°的角,拉绳PC在地面α上的射影AC的长是8m.求:
如图所示,8m高旗杆PA直立在地面α上,拉绳PB与地面α成30°的角,拉绳PC在地面α上的射影AC的长是8m.求: